Образец выполнения задания
Тема: Выполнение расчетов с использованием пакета символьной математики MathCAD Цель работы: изучить возможности пакета символьной математики MathCAD в области вычисления математических выражений, использования при расчетах переменных величин различных типов, построения графиков функций, нахождения корней уравнений, решения систем уравнений, решения задач многомерной оптимизации. Теория к лабораторной работе: http://www.exponenta.ru/soft/Mathcad/UsersGuide/0.asp Задание: Выполните расчеты в MathCAD. Образец выполнения задания 1. Вычислите значение выражения:
Решение Введем выражение, используя панель «Калькулятор» (чтобы открыть панель, выберем Вид – Панели инструментов – Калькулятор). По окончании ввода выражения поставим знак «=». Представим результат с тремя знаками после десятичного разделителя. Для этого выполним двойной щелчок мышью по результату и выберем в открывшемся окне «Формат результата»: формат – десятичный; число десятичных знаков – 3.
2. Вычислите значение выражения при z=7:
Решение Опишем переменную z, присвоив ей значение 7:
Введем выражение, используя панель «Калькулятор». По окончании ввода выражения поставим знак «=». Отформатирует результат.
3. Выведите первые 20 членов арифметической прогрессии, заданной своим начальным значением и шагом:
Решение Опишем ранжированную переменную величину i, изменяющуюся от 2 до 20, используя панель «Матрица» и панель «Вычисление» (Вид – Панели инструментов – Матрица; Вид – Панели инструментов – Вычисление).
Введем начальное значение прогрессии и шаг: Опишем арифметическую прогрессию: Выведем значения первых 20 членов прогрессии: a= 4. Дайте символическую оценку предела: Решение Введем предел, используя панель «Исчисление» (Вид – Панели инструментов – Исчисление).
Выполним символическую оценку, используя панель «Вычисление» (Вид – Панели инструментов – Вычисление).
5. Задайте функцию, вычислите ее значение при x=5, постройте график функции:
Решение Зададим функцию:
Вычислим значение функции при х=5:
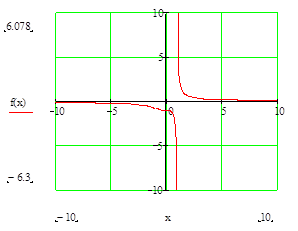
Построим график функции в декартовой системе координат, используя панель «Графики» (Вид – Панели инструментов – Графики). Отформатируем график функции. Для этого выполним двойной щелчок мышью внутри графика и выберем параметры: ось Х – линии сетки; ось Y – линии сетки; стиль осей – пересекающиеся.
6. Решите уравнение несколькими возможными способами:
Решение Опишем уравнение, используя знак «=», который находится на панели «Логический» (Вид – Панели инструментов – Логический).
Найдем решение уравнения. 1 способ: поставим курсор внутри уравнения рядом с переменной, выберем Символика – Переменная – Решить. 2 способ: поставим курсор в конце уравнения (после 1), откроем панель «Символьная» (Вид – Панели инструментов – Символьная), выберем команду solve, введем имя переменной x (относительно которой ищется решение) в появившийся местозаполнитель.
3 способ. Найдем корень уравнения, ближайший к 0. Для этого опишем решение следующим образом:
7. Решите систему уравнений:
Решение Зададим приближение к решению:
Запишем систему, используя знак «=», который находится на панели «Логический»:
Зададим поиск решений, используя символическую оценку:
Варианты заданий Вариант 1 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=5:
3. Выведите первые 20 членов арифметической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=3, постройте график функции:
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: Для изготовления изделий двух видов имеется 100 кг металла. На изготовление одного изделия 1-го вида расходуется 2 кг, а на изделие второго вида – 4 кг металла. Требуется спланировать производство так, чтобы была обеспечена наибольшая прибыль, если отпускная стоимость одного изделия 1-го вида составляет 3 рубля, а изделия 2-го вида – 2 рубля, причем изделий 1-го вида требуется не более 40, а второго вида – не более 20.
Вариант 2 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=3:
3. Выведите первые 20 членов арифметической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=4, постройте график функции:
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: На складах А и В находится по 90 т горючего. Перевозка одной тонны горючего со склада А в пункты 1, 2, 3 соответственно стоит 1, 3, 5 у.е., а перевозка одной тонны со склада В в те же пункты – соответственно 2, 5 и 4 у.е. В каждый пункт надо доставить одинаковое количество тонн горючего. Составить такой план перевозки горючего, при котором транспортные расходы будут наименьшими.
Вариант 3 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=3:
3. Выведите первые 20 членов арифметической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: Необходимо ежедневно с первого склада перевозить в два магазина 50 телевизоров, а со второго склада — 70. При этом первый магазин продает за день 40 телевизоров, а второй — 80. Известны затраты на перевозку телевизоров со складов в магазины (четыре константы: 1200 у.е. при перевозке одного телевизора с первого склада в первый магазин, 1600 — с первого склада во второй магазин, 800 — со второго склада в первый магазин и 1000 — со второго склада во второй магазин). Спрашивается, как нужно организовать перевозки (найти значения переменных x1, x2, x3 и x4), чтобы затраты были минимальны.
Вариант 4 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=3:
3. Выведите первые 20 членов арифметической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: Пусть цех малого предприятия должен изготовить 100 изделий трех типов. Каждого изделия нужно сделать не менее 20 штук. На изделия уходят соответственно 4, 3.4 и 2 кг металла при его общем запасе 340 кг, а также по 4.75, 11 и 2 кг пластмассы при ее общем запасе 700 кг. Сколько изделий каждого типа x1, x2, и x3 надо выпустить для получения максимального объема выпуска в денежном выражении, если цена изделий составляет по калькуляции 4, 3 и 2 у.е.
Вариант 5 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=6:
3. Выведите первые 20 членов арифметической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: Для изготовления изделий двух видов имеется 100 кг металла. На изготовление одного изделия 1-го вида расходуется 2 кг, а на изделие второго вида – 4 кг металла. Требуется спланировать производство так, чтобы была обеспечена наибольшая прибыль, если отпускная стоимость одного изделия 1-го вида составляет 3 рубля, а изделия 2-го вида – 2 рубля, причем изделий 1-го вида требуется не более 40, а второго вида – не более 20.
Вариант 6 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=2:
3. Выведите первые 20 членов арифметической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: На складах А и В находится по 90 т горючего. Перевозка одной тонны горючего со склада А в пункты 1, 2, 3 соответственно стоит 1, 3, 5 у.е., а перевозка одной тонны со склада В в те же пункты – соответственно 2, 5 и 4 у.е. В каждый пункт надо доставить одинаковое количество тонн горючего. Составить такой план перевозки горючего, при котором транспортные расходы будут наименьшими.
Вариант 7 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=10:
3. Выведите первые 20 членов арифметической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: Необходимо ежедневно с первого склада перевозить в два магазина 50 телевизоров, а со второго склада — 70. При этом первый магазин продает за день 40 телевизоров, а второй — 80. Известны затраты на перевозку телевизоров со складов в магазины (четыре константы: 1200 у.е. при перевозке одного телевизора с первого склада в первый магазин, 1600 — с первого склада во второй магазин, 800 — со второго склада в первый магазин и 1000 — со второго склада во второй магазин). Спрашивается, как нужно организовать перевозки (найти значения переменных x1, x2, x3 и x4), чтобы затраты были минимальны. Вариант 8 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=3:
3. Выведите первые 20 членов геометрической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: Пусть цех малого предприятия должен изготовить 100 изделий трех типов. Каждого изделия нужно сделать не менее 20 штук. На изделия уходят соответственно 4, 3.4 и 2 кг металла при его общем запасе 340 кг, а также по 4.75, 11 и 2 кг пластмассы при ее общем запасе 700 кг. Сколько изделий каждого типа x1, x2, и x3 надо выпустить для получения максимального объема выпуска в денежном выражении, если цена изделий составляет по калькуляции 4, 3 и 2 у.е. Вариант 9 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=2:
3. Выведите первые 20 членов геометрической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: Необходимо ежедневно с первого склада перевозить в два магазина 50 телевизоров, а со второго склада — 70. При этом первый магазин продает за день 40 телевизоров, а второй — 80. Известны затраты на перевозку телевизоров со складов в магазины (четыре константы: 1200 у.е. при перевозке одного телевизора с первого склада в первый магазин, 1600 — с первого склада во второй магазин, 800 — со второго склада в первый магазин и 1000 — со второго склада во второй магазин). Спрашивается, как нужно организовать перевозки (найти значения переменных x1, x2, x3 и x4), чтобы затраты были минимальны.
Вариант 10 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=
3. Выведите первые 20 членов геометрической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: На складах А и В находится по 90 т горючего. Перевозка одной тонны горючего со склада А в пункты 1, 2, 3 соответственно стоит 1, 3, 5 у.е., а перевозка одной тонны со склада В в те же пункты – соответственно 2, 5 и 4 у.е. В каждый пункт надо доставить одинаковое количество тонн горючего. Составить такой план перевозки горючего, при котором транспортные расходы будут наименьшими.
Вариант 11 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=4:
3. Выведите первые 20 членов геометрической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: Для изготовления изделий двух видов имеется 100 кг металла. На изготовление одного изделия 1-го вида расходуется 2 кг, а на изделие второго вида – 4 кг металла. Требуется спланировать производство так, чтобы была обеспечена наибольшая прибыль, если отпускная стоимость одного изделия 1-го вида составляет 3 рубля, а изделия 2-го вида – 2 рубля, причем изделий 1-го вида требуется не более 40, а второго вида – не более 20.
Вариант 12 1. Вычислите значение выражения:
2. Вычислите значение выражения при z=3:
3. Выведите первые 20 членов геометрической прогрессии, заданной своим начальным значением и шагом:
4. Дайте символическую оценку предела: 5. Задайте функцию, вычислите ее значение при x=
6. Постройте в одной системе координат графики функции: и для xϵ[-5,5] c шагом 0,1. (образец графика см. на рис.1 в конце документа). 7. Решите уравнение несколькими возможными способами:
8. Решите систему уравнений:
9. Найдите точки экстремумов функций и значения экстремумов: 10. Решите задачу многомерной оптимизации, используя MathCAD: Пусть цех малого предприятия должен изготовить 100 изделий трех типов. Каждого изделия нужно сделать не менее 20 штук. На изделия уходят соответственно 4, 3.4 и 2 кг металла при его общем запасе 340 кг, а также по 4.75, 11 и 2 кг пластмассы при ее общем запасе 700 кг. Сколько изделий каждого типа x1, x2, и x3 надо выпустить для получения максимального объема выпуска в денежном выражении, если цена изделий составляет по калькуляции 4, 3 и 2 у.е.
1. Перечислите названия известных вам пакетов символьной математики. 2. Каковы основные принципы работы пакетов символьной математики? 3. Каким образом описываются переменные величины в пакете MathCAD? 4. Каким образом записываются ранжированные величины в пакете MathCAD? 5. Как построить график функции в MathCAD? 6. Как найти корни уравнения в MathCAD? 7. Как решить в MathCAD систему уравнений?
|

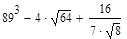
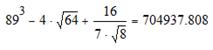
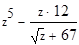
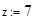
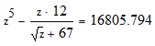
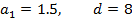
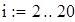
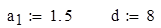
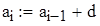
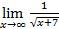

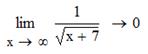
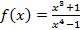
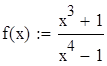
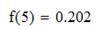
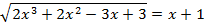
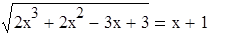
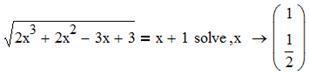
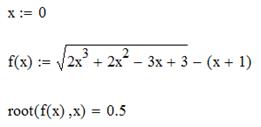
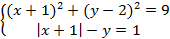

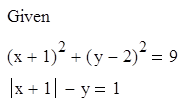
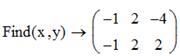

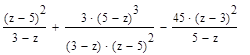

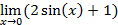
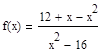
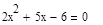
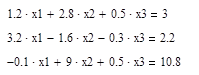
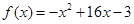 (имеется точка максимума),
(имеется точка максимума),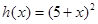 (имеется точка минимума).
(имеется точка минимума).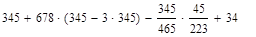
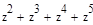

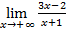
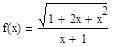
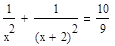
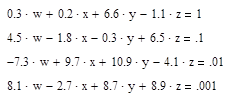
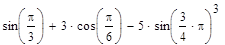
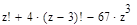

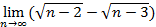
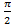 , постройте график функции:
, постройте график функции: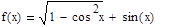
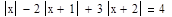

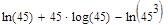
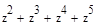


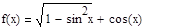
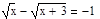
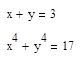
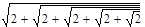
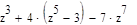

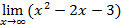
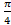 , постройте график функции:
, постройте график функции:
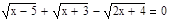
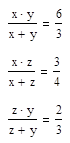
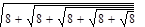
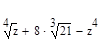

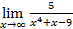
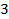 , постройте график функции:
, постройте график функции:
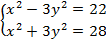
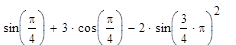


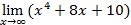
 , постройте график функции:
, постройте график функции: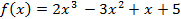
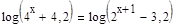
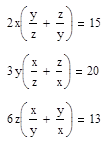
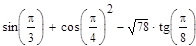
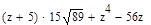

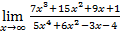
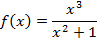
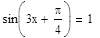
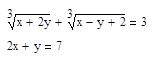
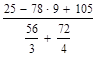
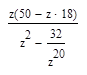

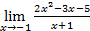
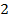 , постройте график функции:
, постройте график функции: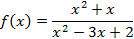

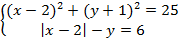

 :
: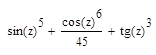

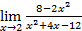
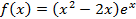
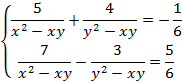
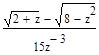
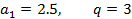
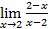

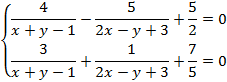
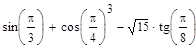
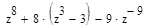


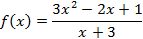

 Контрольные вопросы
Контрольные вопросы



