В данной лекции мы обобщим некоторые определения на случай бесконечных графов. Бесконечным графом называется пара  ,
,  , где
, где  — бесконечное множество элементов, называемое вершинами, а
— бесконечное множество элементов, называемое вершинами, а  — бесконечное семейство неупорядоченных пар элементов из
— бесконечное семейство неупорядоченных пар элементов из  , называемых ребрами.
, называемых ребрами.
Если оба множества  и
и  — счетны, то
— счетны, то  называется счетным графом. Заметим, что наши определения исключают те случаи, когда
называется счетным графом. Заметим, что наши определения исключают те случаи, когда  — бесконечно, а
— бесконечно, а  — конечно. Такие объекты являются всего лишь конечными графами с бесконечным множеством изолированных вершин. Когда
— конечно. Такие объекты являются всего лишь конечными графами с бесконечным множеством изолированных вершин. Когда  — бесконечно, а
— бесконечно, а  — конечно, такие объекты являются конечными графами с бесконечным числом петель или кратных ребер.
— конечно, такие объекты являются конечными графами с бесконечным числом петель или кратных ребер.
Некоторые определения таких понятий, как "смежный", " инцидентный ", "изоморфный", " подграф ", " объединение ", "связный", "компонента" переносятся на бесконечные графы. Степенью вершины 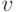 бесконечного графа называется мощность множества ребер, инцидентных
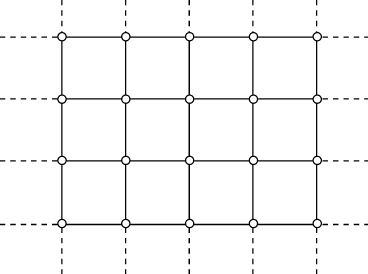
бесконечного графа называется мощность множества ребер, инцидентных 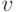 Степень вершины может быть конечной или бесконечной. Бесконечный граф, все вершины которого имеют конечные степени, называется локально конечным. Хорошо известным примером такого графа является бесконечная квадратная решетка, часть которой изображена на рисунке. Локально счетный бесконечный граф — это граф, все вершины которого имеют счетную степень. Под счетным множеством здесь и в дальнейшем понимается бесконечное множество, допускающее взаимно однозначное отображение на множество натуральных чисел.
Степень вершины может быть конечной или бесконечной. Бесконечный граф, все вершины которого имеют конечные степени, называется локально конечным. Хорошо известным примером такого графа является бесконечная квадратная решетка, часть которой изображена на рисунке. Локально счетный бесконечный граф — это граф, все вершины которого имеют счетную степень. Под счетным множеством здесь и в дальнейшем понимается бесконечное множество, допускающее взаимно однозначное отображение на множество натуральных чисел.
Теорема Каждый связный локально счетный бесконечный граф является счетным.

 ,
,  , где
, где  — бесконечное множество элементов, называемое вершинами, а
— бесконечное множество элементов, называемое вершинами, а  — бесконечное семейство неупорядоченных пар элементов из
— бесконечное семейство неупорядоченных пар элементов из 
 называется счетным графом. Заметим, что наши определения исключают те случаи, когда
называется счетным графом. Заметим, что наши определения исключают те случаи, когда 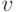 бесконечного графа называется мощность множества ребер, инцидентных
бесконечного графа называется мощность множества ребер, инцидентных 


