Если 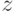 — произвольная вершина графа
— произвольная вершина графа  , отличная от
, отличная от 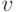 , то существует нетривиальная простая цепь от
, то существует нетривиальная простая цепь от 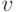 до
до 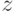 , отсюда следует, что в
, отсюда следует, что в  имеется бесконечно много простых цепей с начальной вершиной
имеется бесконечно много простых цепей с начальной вершиной 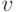 . Поскольку степень
. Поскольку степень 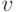 конечна, то бесконечное множество таких простых цепей должно начинаться с одного и того же ребра. Если таким ребром является
конечна, то бесконечное множество таких простых цепей должно начинаться с одного и того же ребра. Если таким ребром является  , то, повторяя эту процедуру для вершины
, то, повторяя эту процедуру для вершины 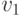 , получим новую вершину
, получим новую вершину 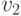 и соответствующее ей ребро
и соответствующее ей ребро  . Продолжая таким образом, получим бесконечную в одну сторону простую цепь
. Продолжая таким образом, получим бесконечную в одну сторону простую цепь  .
.
Важное значение леммы Кенига состоит в том, что она позволяет получить результаты о бесконечных графах из соответствующих результатов для конечных графов. Типичным примером является следующая теорема.
Теорема 6.2. Пусть  — счетный граф, каждый конечный подграф которого планарен, тогда и
— счетный граф, каждый конечный подграф которого планарен, тогда и  планарен.
планарен.
Доказательство Так как  — счетный граф, его вершины можно занумеровать в последовательность
— счетный граф, его вершины можно занумеровать в последовательность 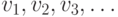 . Исходя из нее, построим строго возрастающую последовательность
. Исходя из нее, построим строго возрастающую последовательность 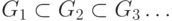 подграфов графа
подграфов графа  , выбирая в качестве
, выбирая в качестве  подграф с вершинами
подграф с вершинами  и ребрами графа
и ребрами графа  , соединяющими только эти вершины между собой. Далее, примем на веру тот факт, что графы
, соединяющими только эти вершины между собой. Далее, примем на веру тот факт, что графы 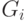 могут быть уложены на плоскости конечным числом, скажем
могут быть уложены на плоскости конечным числом, скажем 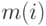 , топологически различных способов, и построим еще один бесконечный граф
, топологически различных способов, и построим еще один бесконечный граф 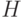 . Его вершины
. Его вершины  ,
,  пусть соответствуют различным укладкам графов
пусть соответствуют различным укладкам графов  , а его ребра соединяют те из вершин
, а его ребра соединяют те из вершин  и
и 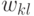 , для которых
, для которых 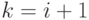 и плоская укладка, соответствующей
и плоская укладка, соответствующей  . Мы видим, что граф
. Мы видим, что граф 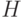 связен и локально конечен, поэтому, как следует из леммы Кенига, он содержит бесконечную в одну сторону простую цепь. А так как граф
связен и локально конечен, поэтому, как следует из леммы Кенига, он содержит бесконечную в одну сторону простую цепь. А так как граф  является счетным, то эта бесконечная простая цепь и дает требуемую плоскую укладку графа
является счетным, то эта бесконечная простая цепь и дает требуемую плоскую укладку графа  .
.
Стоит подчеркнуть, что если принять дальнейшие аксиомы теории множеств, в частности, аксиому выбора для несчетных множеств, то многие результаты можно перенести и на такие бесконечные графы, которые необязательно являются счетными.

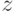 — произвольная вершина графа
— произвольная вершина графа  , отличная от
, отличная от 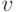 , то существует нетривиальная простая цепь от
, то существует нетривиальная простая цепь от  , то, повторяя эту процедуру для вершины
, то, повторяя эту процедуру для вершины 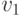 , получим новую вершину
, получим новую вершину 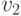 и соответствующее ей ребро
и соответствующее ей ребро  . Продолжая таким образом, получим бесконечную в одну сторону простую цепь
. Продолжая таким образом, получим бесконечную в одну сторону простую цепь  .
.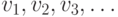 . Исходя из нее, построим строго возрастающую последовательность
. Исходя из нее, построим строго возрастающую последовательность 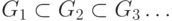 подграфов графа
подграфов графа  подграф с вершинами
подграф с вершинами  и ребрами графа
и ребрами графа 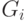 могут быть уложены на плоскости конечным числом, скажем
могут быть уложены на плоскости конечным числом, скажем 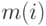 , топологически различных способов, и построим еще один бесконечный граф
, топологически различных способов, и построим еще один бесконечный граф 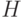 . Его вершины
. Его вершины  ,
,  пусть соответствуют различным укладкам графов
пусть соответствуют различным укладкам графов  , а его ребра соединяют те из вершин
, а его ребра соединяют те из вершин  и
и 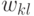 , для которых
, для которых 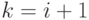 и плоская укладка, соответствующей
и плоская укладка, соответствующей 


