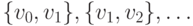Пусть 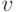 — произвольная вершина такого бесконечного графа, и пусть
— произвольная вершина такого бесконечного графа, и пусть 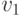 — множество вершин, смежных
— множество вершин, смежных 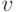 ,
, 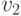 — множество всех вершин, смежных вершинам из
— множество всех вершин, смежных вершинам из 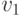 , и т.д. По условию теоремы
, и т.д. По условию теоремы 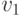 — счетно и, следовательно, множества
— счетно и, следовательно, множества  тоже счетны. Здесь используется тот факт, что объединение не более чем счетного множества счетных множеств счетно. Следовательно,
тоже счетны. Здесь используется тот факт, что объединение не более чем счетного множества счетных множеств счетно. Следовательно,  — последовательность множеств, объединение которых счетно. Кроме того, эта последовательность содержит каждую вершину бесконечного графа в силу его связности. Отсюда и следует нужный результат.
— последовательность множеств, объединение которых счетно. Кроме того, эта последовательность содержит каждую вершину бесконечного графа в силу его связности. Отсюда и следует нужный результат.
Следствие Каждый связный локально конечный бесконечный граф является счетным.
Помимо этого, на бесконечный граф  можно перенести понятие маршрута, причем тремя различными способами:
можно перенести понятие маршрута, причем тремя различными способами:
1. Конечный маршрут в  определяется так. Маршрутом в данном графе
определяется так. Маршрутом в данном графе  называется конечная последовательность ребер вида
называется конечная последовательность ребер вида  ,
,  . Маршрут можно обозначить и так:
. Маршрут можно обозначить и так:  .
.
2. Бесконечным в одну сторону маршрутом в  с начальной вершиной
с начальной вершиной  называется бесконечная последовательность ребер вида
называется бесконечная последовательность ребер вида  ,
, 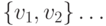 .
.
3. Бесконечным в обе стороны маршрутом в графе  называется бесконечная последовательность ребер вида
называется бесконечная последовательность ребер вида  ,
, 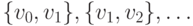
Бесконечные в одну сторону и в обе стороны цепи и простые цепи определяются очевидным образом, так же как и понятия длины цепи и расстояния между вершинами. Бесконечные простые цепи не так уж трудно обнаружить.
Теорема 6.1. (Кениг, 1936) Пусть  — связный локально конечный бесконечный граф, тогда для любой вершины
— связный локально конечный бесконечный граф, тогда для любой вершины 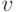 существует бесконечная в одну сторону простая цепь с начальной вершиной
существует бесконечная в одну сторону простая цепь с начальной вершиной 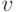 .
.

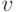 — произвольная вершина такого бесконечного графа, и пусть
— произвольная вершина такого бесконечного графа, и пусть 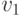 — множество вершин, смежных
— множество вершин, смежных 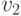 — множество всех вершин, смежных вершинам из
— множество всех вершин, смежных вершинам из  тоже счетны. Здесь используется тот факт, что объединение не более чем счетного множества счетных множеств счетно. Следовательно,
тоже счетны. Здесь используется тот факт, что объединение не более чем счетного множества счетных множеств счетно. Следовательно,  — последовательность множеств, объединение которых счетно. Кроме того, эта последовательность содержит каждую вершину бесконечного графа в силу его связности. Отсюда и следует нужный результат.
— последовательность множеств, объединение которых счетно. Кроме того, эта последовательность содержит каждую вершину бесконечного графа в силу его связности. Отсюда и следует нужный результат. можно перенести понятие маршрута, причем тремя различными способами:
можно перенести понятие маршрута, причем тремя различными способами: ,
,  . Маршрут можно обозначить и так:
. Маршрут можно обозначить и так:  .
. называется бесконечная последовательность ребер вида
называется бесконечная последовательность ребер вида 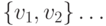 .
. ,
,