Завдання та методичні рекомендації до вивчення теми. Докладно питання побудови різних регресій (парних та множинних лінійних, квазілінійних, нелінійних відносно факторів і параметрів
Докладно питання побудови різних регресій (парних та множинних лінійних, квазілінійних, нелінійних відносно факторів і параметрів, з фіктивними змінними) розглянуті в навчально-методичному посібнику «Економіко-математичні методи та моделі. Частина 2» [4]. Повторимо основні етапи побудови і аналізу лінійної парної регресії на прикладі. Приклад. Дохід підприємства Y (тис. грн.) наведено в таблиці:
Побудуємо діаграму розподілу на основі даних спостережень. Точки спостережень групуються навколо вдаваної прямої (див. рис. на с.11, розрахунок – на с. 12). Тому припустимо, що дані спостережень наближено можна описати лінійною залежністю між фактором Х та показником Y. Побудуємо парну лінійну регресійну модель:
де
Параметри
За допомогою вказаного методу отримані значення параметрів:
де Отже, розрахункові значення показника обчислюються за формулою:
Середньоквадратична помилка регресії:
Відносно середнього вибіркового значення Коефіцієнт кореляції R обчислюється за формулою:
Для даної моделі R=0,94 означає, що між фактором та показником існує тісний додатний зв'язок. Коефіцієнт детермінації для даної моделі дорівнює
Таким чином, згідно з обраною моделлю, залежність показника Y пояснюється саме фактором Х, залученим у модель, з урахуванням специфікації моделі, на 89 %. Перевіримо адекватність побудованої лінійної моделі за критерієм Фішера. Для цього розрахуємо значення F-критерію згідно з моделлю:
За статичними таблицями F-розподілу Фішера для 5%-ого рівня значимості (задаємо довільно) та при степенях вільності відповідно 1 (для парної регресії) і n- 2=7 знайдемо критичне значення Із двох оцінених параметрів саме параметр
де Критичне значення t-статистики знаходимо за статистичними таблицями t-розподілу Стьюдента при рівні значимості Таким чином, розрахункове значення більше, ніж критичне. Отже, параметр Для оцінки впливу фактора Х на показник Y без урахування одиниць виміру обчислимо коефіцієнти еластичності для кожного спостереження за формулою
та побудуємо діаграму. Як бачимо, еластичність обсягу реалізації продукції збільшується при збільшенні затрат на рекламу. Еластичність, що обчислена на основі середніх значень показника і фактора, складає
Це означає, що якщо фактор зміниться на 1%, то показник зміниться на 0,888%. Модель є адекватною, як було показано, зі статистично значимим параметром Точкову оцінку отримаємо за формулою:
Далі побудуємо надійний інтервал з границями (
Границі довірчого інтервалу (11021,06; 16510,39) (тис. грн.) встановлені з надійністю 95%.
Рис. 1 – Регресія, довірча зона і прогнозні оцінки доходу
Рис.2 – Коефіцієнт еластичності доходу
Якщо виникає потреба розглядати залежність показника від декількох факторів, треба будувати множинну регресію:
де або для
В моделі мають бути присутніми тільки незалежні фактори. Одним із методів визначення наявності чи відсутності мультиколінеарності (залежності факторів) є побудова матриці парних коефіцієнтів кореляції:
Матриця має властивості: діагональні елементи дорівнюють одиниці; матриця симетрична відносно головної діагоналі. Для розрахунку коефіцієнтів парної кореляції можна користуватися функцією КОРРЕЛ. Для кожної пари факторів визначають коефіцієнт парної кореляції. Якщо значення коефіцієнта кореляції близько за модулем до одиниці, то між цими факторами існує тісний зв'язок, тобто фактори залежні. Треба виключити один з цих факторів. Виключають той, що має менший вплив на показник, про що свідчать коефіцієнти кореляції між факторами та показником (у першому рядку матриці). Параметри регресії визначаються у матричному вигляді наступним чином:
де
Для зменшення степені залежності коефіцієнту детермінації від кількості факторів використовують оцінений коефіцієнт детермінації:
Для перевірки адекватності моделі використовується критерій Фішера, для визначення значимості параметрів регресії – критерій Стьюдента. Розрахункові значення можна отримати за формулами:
Для визначення меж довірчих інтервалів показника існує формула: (
де Використання деяких функцій в електронних таблицях EXCEL для розрахунку статистики і перевірки лінійної регресійної моделі Для розрахунку параметрів та статистики моделі можна користуватися статистичною функцією ЛИНЕЙН:
ЛИНЕЙН (известные_значения_y;известные_значения_x;конст;статистика) Для даної задачі: известные_значения_y – значення обсягу реалізації продукції (масив значень У) известные_значения_x – значення витрат на рекламу (масив значеньХ) конст – значення, яке показує, чи необхідно, щоб константа мала нульове значення (конст має значення ЛОЖЬ, задається значення 0), чи щоб константа обчислювалася звичайним способом (конст має значення ИСТИНА, задається значення 1). статистика – значення, яке показує, чи необхідно, щоб виводилась додаткова статистика по регресії (конст має значення ИСТИНА, задається значення 1) або треба вивести тільки значення параметрів регресії (конст має значення ЛОЖЬ, задається значення 0). Регресійна статистика має вигляд:
де
Для розрахунку за допомогою функції ЛИНЕЙН треба виконати такі дії: 1) викликати функцію ЛИНЕЙН (fx); 2) у вікні функції задати значення Х (незалежної змінної - фактора) та значення У (залежної змінної – показника); також задати значення статистики (1) та константи (1); Ок; 3) виділити область: кількість стовпчиків дорівнює кількості параметрів регресії; кількість рядків завжди однакова: 5; 4) натиснути функціональну клавішу F2; 5) натиснути одночасно клавіші Ctrl, Shift, Enter. Критичне значення критерію Фішера знаходяться за допомогою функції FРАСПОБР (α; р; n-р-1) для надійності та при р факторах, n – кількість спостережень, Критичне значення критерію Стьюдента обчислюється за допомогою функції СТЬЮДРАСПОБР (α; n-р-1) для надійності 1- α, n – кількість спостережень, р – кількість факторів. Для визначення добутку матриць можна користуватися функцією МУМНОЖ,для обчислення оберненої матриці - функцією МОБР,для транспонування матриць – функцією ТРАНСП.
Перетворення нелінійних моделей докладно розглянуто в навчально-методичному посібнику «Економіко-математичні методи та моделі. Частина 2» [4].
Питання для самоконтролю 1. Наведіть приклади застосування регресійних моделей в аналізі фінансової діяльності підприємств. 2. В чому полягає економічна сутність кривої Лаффера? 3. Наведіть приклади застосування моделей з фіктивними змінними для аналізу економічних та фінансових процесів.
Завдання до самостійної роботи
Завдання 1 Дослідження безробіття в Дніпропетровській області Розглянути дві однофакторні моделі: динаміку зміни показників безробіття та зв'язок між показниками безробіття та середньою заробітною платою. Обрати правильну специфікацію моделей. Провести аналіз моделей економетричними методами при рівнях значимості 0.05 та 0.1. Зробити висновки. Порівняти розв’язки. Визначити прогнозні оцінки показників на 2011 та 2012 роки (при обох рівнях значимості). Дані наведено в таблиці:
Завдання 2 Виконання фінансування державних та місцевих програм на соціальний захист населення (на прикладі Індустріального району м. Дніпропетровська) Дослідження провести для двох категорій окремо: · соціальна допомога на догляд за дитиною до 3-х років; · соціальна допомога малозабезпеченим сім’ям. Обрати найкращу функцію для апроксимації вихідних даних (наприклад, квадратичну). Оцінити параметри моделей, адекватність в цілому та статистичну значимість параметрів. Побудувати регресії залежності соціальної допомоги від загальної суми субвенцій та динаміку соціальної допомоги. Визначити точкову та інтервальну оцінки для прогнозу соціальної допомоги на 2011 рік. Зробити висновки. Дані наведені нижче:
Завдання 3 Дослідження фінансових показників діяльності банку (на прикладі Приватбанку) Визначити залежність кредитування та виплачених відсотків за депозитами від залучених депозитів. Дані наведено нижче. Обрати специфікацію моделі. Зробити аналіз економетричними методами. Побудувати довірчі зони регресій (обрати рівень значимості самостійно) та пояснити результати. Зробити висновки
Завдання 4 Обсяг перевезень товарів за три роки в залежності від кварталу представлено у таблиці:
Побудувати модель перевезень за допомогою фіктивних змінних та звичайну парну модель лінійної регресії. Порівняти результати. Побудувати графіки для обох моделей. Знайти оцінки прогнозу (точкову та інтервальну) обсягу перевезень товарів для третього кварталу наступного року.
Рекомендована література [4, 7, 9, 11]
|

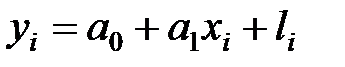 ,
,  (1)
(1)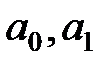 – параметри, які треба визначити;
– параметри, які треба визначити; – відхилення фактичних значень
– відхилення фактичних значень 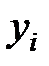 від їх оцінки
від їх оцінки 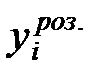 ;
; - кількість спостережень.
- кількість спостережень.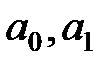 визначимо методом найменших квадратів, згідно з яким, сума квадратів різниць
визначимо методом найменших квадратів, згідно з яким, сума квадратів різниць  має бути мінімальною для найкращого наближення, яке забезпечує регресія, тобто
має бути мінімальною для найкращого наближення, яке забезпечує регресія, тобто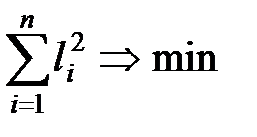 .
. =-2259807,1, (2)
=-2259807,1, (2)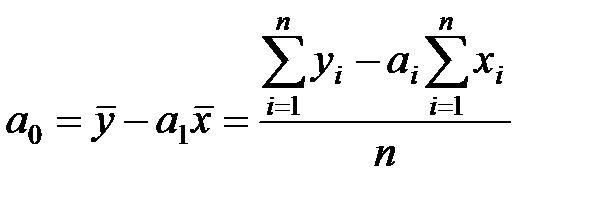 = 1129,445, (3)
= 1129,445, (3)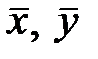 - середні значення вибіркових даних.
- середні значення вибіркових даних. -2259807,1 + 1129,445 хі.
-2259807,1 + 1129,445 хі. = 1172,05. (4)
= 1172,05. (4) = 8118,5 це становить 14,4 %.
= 8118,5 це становить 14,4 %. . (5)
. (5)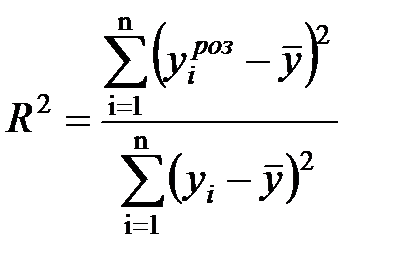 = 0,89. (6)
= 0,89. (6) 55,72. (7)
55,72. (7) 5,59. Таким чином, розраховане значення F більше, ніж критичне. Отже, можна зробити висновок про адекватність побудованої моделі вихідним даним за F-критерієм Фішера.
5,59. Таким чином, розраховане значення F більше, ніж критичне. Отже, можна зробити висновок про адекватність побудованої моделі вихідним даним за F-критерієм Фішера. визначає степінь залежності показника від фактора. Тому перевіримо його статистичну значимість. Це можна зробити за допомогою критерію Стьюдента. Розрахункове значення t-статистики отримаємо як відношення
визначає степінь залежності показника від фактора. Тому перевіримо його статистичну значимість. Це можна зробити за допомогою критерію Стьюдента. Розрахункове значення t-статистики отримаємо як відношення  :
: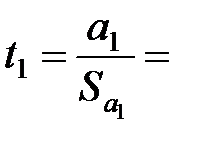 7,46, (8)
7,46, (8)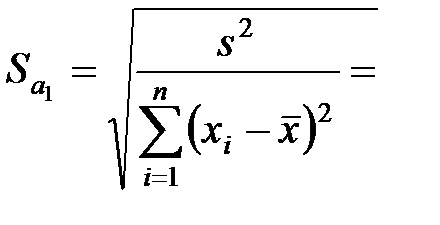 151,3,
151,3,  . (9)
. (9) 0,1 (задаємо довільно) та ступенях вільності n- 2= 7:
0,1 (задаємо довільно) та ступенях вільності n- 2= 7: 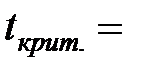 1,89.
1,89.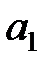 з надійністю 95% (1-α/2) можна вважати статистично значимим.
з надійністю 95% (1-α/2) можна вважати статистично значимим.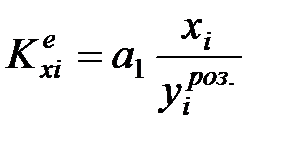 (10)
(10)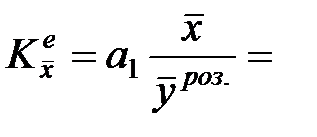 0,888.
0,888. . Тому її можна використовувати для прогнозування доходу підприємства. Визначимо прогноз на наступний 2013 рік.
. Тому її можна використовувати для прогнозування доходу підприємства. Визначимо прогноз на наступний 2013 рік.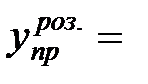 -2259807,1 + 1129,445 хпр = 13765,725 (тис. грн.).
-2259807,1 + 1129,445 хпр = 13765,725 (тис. грн.). ;
;  ), де
), де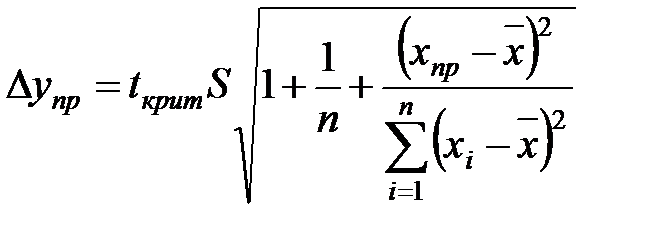 = 2744,67. (11)
= 2744,67. (11)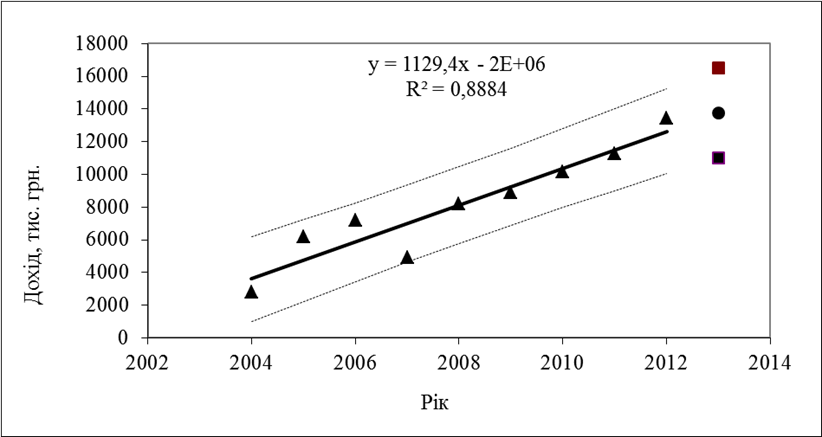

 , (12)
, (12)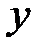 - показник,
- показник,  - фактори,
- фактори, 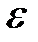 - випадкова величина,
- випадкова величина, го спостереження,
го спостереження, 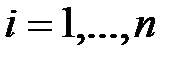 :
: . (13)
. (13) . (14)
. (14)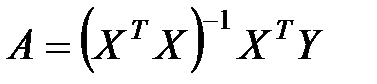 , (15)
, (15) - матриця спостережень за незалежними змінними;
- матриця спостережень за незалежними змінними;
 - матриця, транспонована до матриці
- матриця, транспонована до матриці  ;
; - матриця, обернена до матриці
- матриця, обернена до матриці  ;
; - матриця спостережень за показником
- матриця спостережень за показником  ;
; - матриця параметрів регресії;
- матриця параметрів регресії;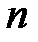 - кількість спостережень,
- кількість спостережень, 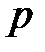 - кількість факторів.
- кількість факторів.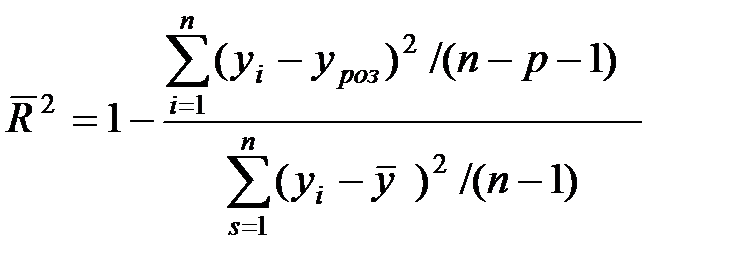 . (16)
. (16) ;
;  . (17)
. (17)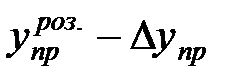 ;
; 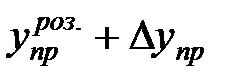 ),
),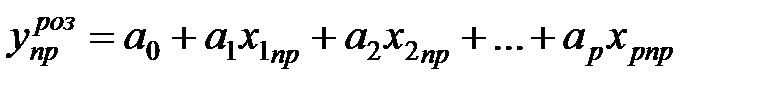 , (18)
, (18) , (19)
, (19) , (20)
, (20) .
.


