Завдання та методичні рекомендації до вивчення теми. Постановка задач лінійного програмування (пряма і двоїста), а також методи розв’язування докладно розглядалися в дисципліні «Економіко-математичні методи та
Постановка задач лінійного програмування (пряма і двоїста), а також методи розв’язування докладно розглядалися в дисципліні «Економіко-математичні методи та моделі. Частина 1» [3]. Можна також звернутися до літератури, що вказана до даної теми. До задач, що використовують оптимізаційні методи, можна віднести задачі складання оптимального плану виробництва продукції, оптимального складу портфеля цінних паперів, раціонального розподілу робітників на виробництві і т.ін. Часто на практиці використовуються сполуки моделей, наприклад, економетричних для побудови залежності між показником та факторами, і далі оптимізаційних, для яких використовуються методи лінійного або нелінійного математичного програмування. Для прикладу розглянемо спочатку задачу оптимізації споживчого вибору [1]. Споживач завжди прагне максимізувати свою корисність, але його стримує обмежений дохід, тобто задачею вибору споживача (задача раціональної поведінки споживача на ринку) є вибір такого споживацького набору, який максимізує його функцію корисності при заданому бюджетному обмеженні.
Формально, цю задачу можна записати у вигляді:
при обмеженнях:
де М – доход, який споживач має намір повністю витратити на придбання споживацького набору для досягнення максимальної корисності, рі – ціна і -го блага. Перше обмеження – бюджетне – встановлює максимальну вартість споживацького набору, друге обмеження витікає з умови, що такі економічні змінні, як кількість благ, не можуть бути від’ємними. У випадку двох благ бюджетне обмеження має вигляд трикутника. Оптимальний розв’язок співпадає з точкою дотику лінії обмеження і лінії байдужості. Отже, треба знайти такий невід’ємний набор благ Математично, це є задача на умовний екстремум з обмеженнями, яку можна звести до задачі на безумовний екстремум функції Лагранжа, яка має вигляд:
Необхідні умови існування безумовного екстремуму:
звідки: Знайдений із цієї системи розв’язок Із перших n рівнянь останньої системи витікає:
Тобто споживач за фіксованого доходу обирає такий набір благ Приклад. Визначити, який набір товарів обере споживач, який має дохід у 300 гр.од., якщо його функція корисності має вигляд
а ціни товарів відповідно дорівнюють: р1 = 2 гр.од.,: р2 = 4 гр.од.,: р3 = 1 гр.од. за одну одиницю. Знайти граничну норму заміни другого товару першим. Розв’язування. Математична постановка задачі: Знайти кількість товарів при бюджетному обмеженні:
Запишемо функцію Лагранжа
Розв’язування вихідної задачі зводиться до визначення такого набору значень Із необхідних умов екстремуму функції Лагранжа маємо: Гранична норма заміни другого товару першим:
тобто, для заміни одиниці другого товару необхідно 2 одиниці першого.
Тепер розглянемо задачу у сфері виробництва [1]. Виробник розв’язує основну задачу максимізації прибутку, тобто максимального випуску за визначених витрат, а також мінімізацію витрат за визначеного об’єму випуску. Нехай виробнича фірма випускає один продукт. Річний випуск позначимо через У. Можливі витрати різних видів ресурсів позначимо через вектор-стовпчик Тоді технологія фірми визначається її виробничою функцією:
Нехай
де
Якщо не вводити ніяких обмежень, окрім невід’ємності витрат, то задача на максимум прибутку виглядає так:
Це задача математичного програмування з n умовами: Необхідними умовами її розв’язування є умови Куна-Таккера:
Якщо використовуються всі ресурси, тобто
Таким чином, в оптимальній точці коштовність граничного продукту даного ресурсу дорівнює його ціні. Аналогічний за формою розв’язок має задача на максимум випуску за заданих витрат:
За допомогою функції Лагранжа
ця задача зводиться до задачі визначення максимуму, для якої умови Куна-Таккера мають вигляд:
звідки
Розглянемо задачу максимізації обсягу продукції, що випускається, при обмеженні витрат на придбання ресурсів (факторів) у випадку двох ресурсів:
за умови, що Розв’язування цієї задачі математичного програмування допускає наочну геометричну інтерпретацію. Обмеженням відповідає трикутник під прямою, яка має рівняння Геометричний розв’язок задачі очевидний: ізокванта та ізокоста, що відповідає фіксованим витратам виробництва С, будуть мати лише одну спільну точку Координати Точка дотику залежить від значення витрат виробництва С. Безліч точок Таким чином, математично маємо задачу на умовний екстремум функції
за наявності обмежень:
Рис. 2 Геометричний розв’язок задачі виробника Поставлену задачу можна звести до задачі на безумовний екстремум функції Лагранжа:
Для функції Лагранжа запишемо систему рівнянь (необхідні умови існування безумовного екстремуму фунції кількох змінних)
або Розв'язавши рівняння щодо шуканих змінних, визначаємо точку Приклад. Випуск фірми, що виробляє один продукт, задається виробничою функцією Кобба-Дугласа:
Визначити максимальний випуск, якщо на оренду фондів та оплату праці виділено 150 ум. од., вартість оренди одиниці фондів Розв’язування. Задачу можна записати наступним чином:
за обмежень:
Оскільки Складемо систему рівнянь: Враховуючи вигляд функції
Розділимо перше рівняння на друге, враховуючи ціни ресурсів, та додамо обмеження:
Розв’язком системи рівнянь є: Визначеному розв’язку відповідає максимальний випуск:
Гранична норма заміни праці фондами визначається як:
тобто один робітник може бути замінений двома одиницями фондів. Моделі та задачі транспортного і розподільчого типів В будь-якій сфері бізнесу прийняття рішень – одна з основних сторін діяльності сучасного менеджера. В простих випадках рішення приймається на основі досвіду та інтуїції. Однак у складних випадках, коли функціонування об’єкту залежить від багатьох факторів, а досягти цілі можна різними путями, то потрібен докладний аналіз проблеми, заснований на кількісних оцінках ефективності рішень, які приймаються. До задач оптимального типу, які пов’язані з вибором оптимального розв’язку, відносяться задачі формування оптимальних виробничих програм, моделі і задачі транспортного типу, моделі і задачі розподільчого типу, моделі оптимального розподілу фінансів. Всі ці задачі відносяться до лінійних задач математичного програмування і розв’язуються відповідними методами: графічним, симплекс-методом, потенціалів і т.д. Складається цільова функція, яка має набути максимуму чи мінімуму за певних обмежень. Ці методи і відповідні приклади розглядалися в навчально-методичному посібнику з дисципліни «Економіко-математичні методи та моделі. Частина 1» [3]. Для пошуку оптимального розв’язку можна використовувати стандартні процедури «Подбор параметра» і «Поиск решения» в електронних таблицях EXCEL, які розглядалися в дисципліні «Інформатика». Для задач розподільчого типу використовують транспортні алгоритми. Особливістю є те, що змінні – бінарні – можуть приймати тільки два значення: 0 або 1. Питання для самоконтролю 1. Лінійне програмування: постановка прямої і двоїстої задач. Аналіз оптимального розв’язку. 2. Нелінійне програмування та методи розв’язування відповідних задач. 3. Розв’язок задачі оптимізації споживчого вибору з бюджетним обмеженням. 4. Задача виробника та її розв’язування. 5. Дослідження виробничих функцій. 6. Середня та гранична продуктивність ресурсів. Заміщення ресурсів. 7. Задачі розподільчого типу та їх розв’язування за допомогою стандартних процедур. Завдання до самостійної роботи
|


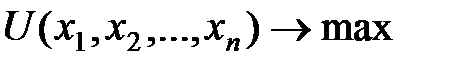 (44)
(44)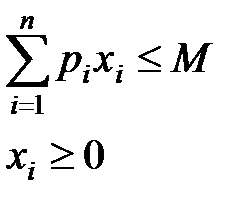 , (45)
, (45)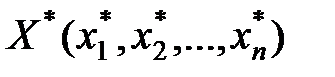 , який принесе споживачу максимум корисності при існуючому бюджетному обмеженні.
, який принесе споживачу максимум корисності при існуючому бюджетному обмеженні.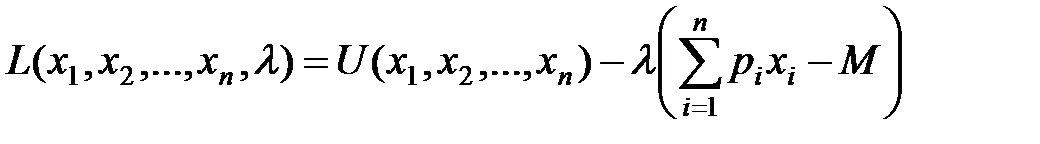 . (46)
. (46)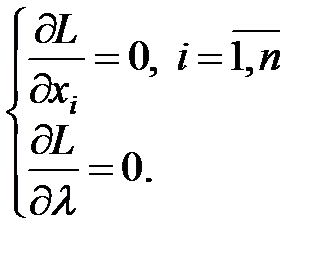 (47)
(47) (48)
(48)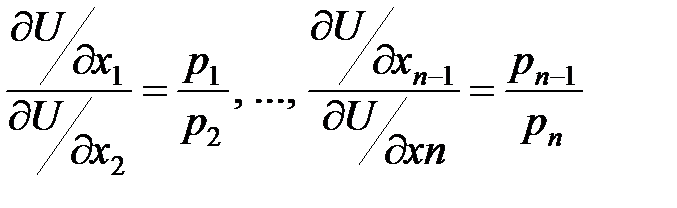 . (49)
. (49)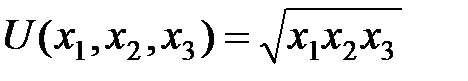 ,
,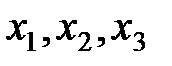 таку, щоб
таку, щоб 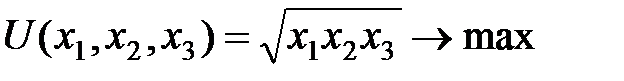
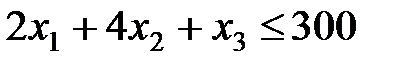
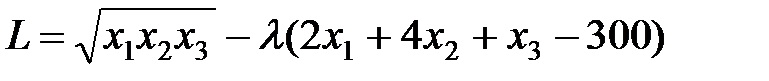
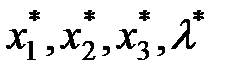 , за якого функція Лагранжа буде мати максимум.
, за якого функція Лагранжа буде мати максимум.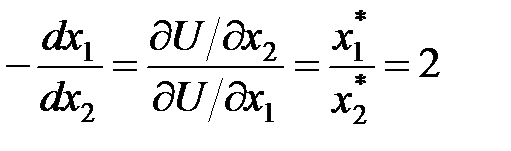 ,
,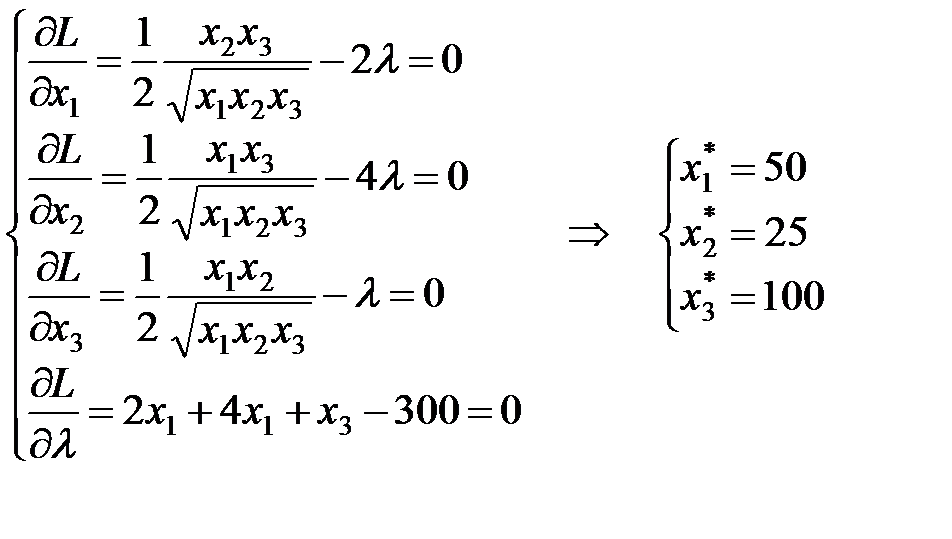
 .
.
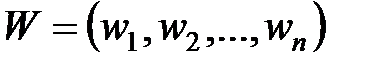 - вектор-рядок цін ресурсів, р – ціна продукції. Тоді кожному вектору витрат Х відповідає прибуток:
- вектор-рядок цін ресурсів, р – ціна продукції. Тоді кожному вектору витрат Х відповідає прибуток: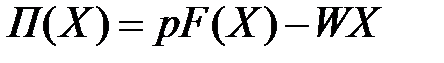 , (50)
, (50)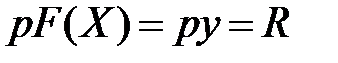 – річний дохід фірми,
– річний дохід фірми,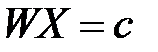 –витрати виробництва за рік.
–витрати виробництва за рік.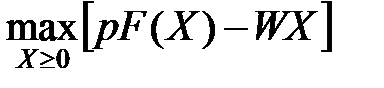 . (51)
. (51)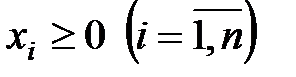 .
.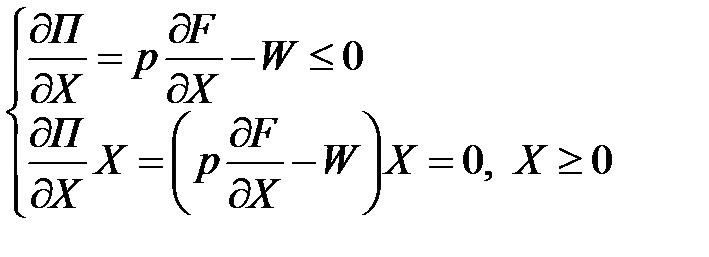 . (52)
. (52) , то ці умови мають вигляд:
, то ці умови мають вигляд: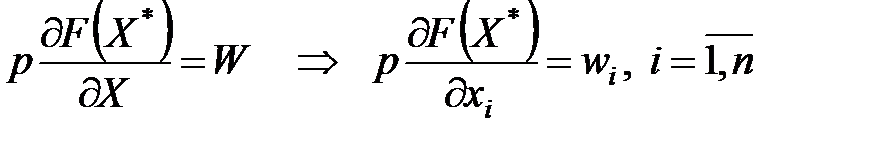 (53)
(53) (34)
(34)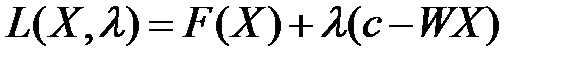 (55)
(55)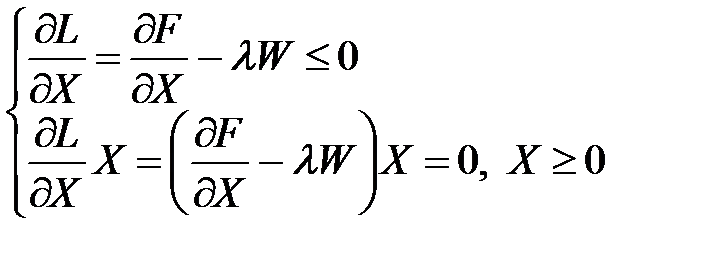 , (56)
, (56)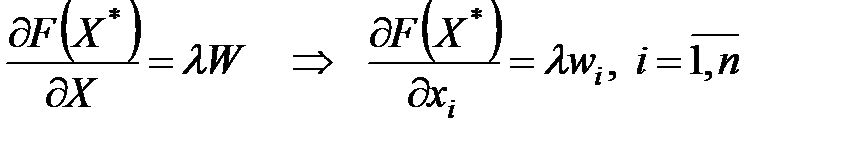 . (57)
. (57) (58)
(58)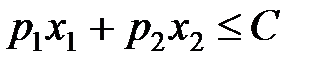 ,
, 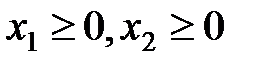 . (59)
. (59)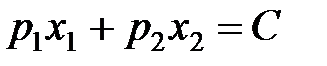 , яке є ізокостою. При максимізації функції ізокванти пересуваються у "північно-східному" напрямку, поки вони мають загальні точки із зазначеним трикутником обмежень.
, яке є ізокостою. При максимізації функції ізокванти пересуваються у "північно-східному" напрямку, поки вони мають загальні точки із зазначеним трикутником обмежень. .
. точки
точки 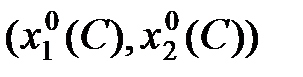 , що відповідають різним значенням витрат, утворять лінію L, що називається довгостроковою лінією розвитку фірми. Точка
, що відповідають різним значенням витрат, утворять лінію L, що називається довгостроковою лінією розвитку фірми. Точка 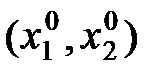 локальної ринкової рівноваги фірми обов'язково належить цій лінії.
локальної ринкової рівноваги фірми обов'язково належить цій лінії.
 , (60)
, (60) .
.
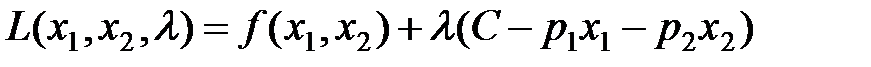 . (61)
. (61)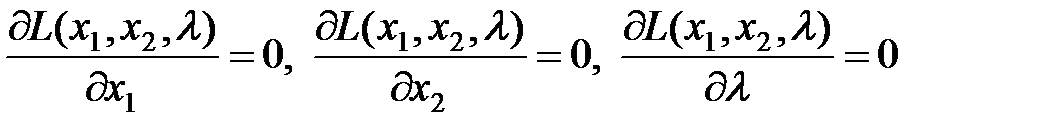
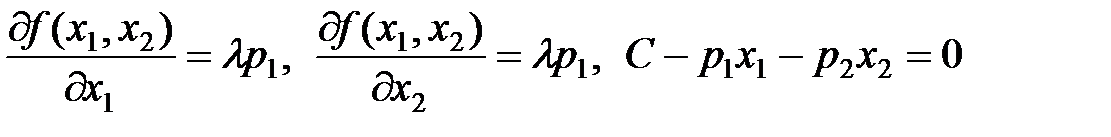 . (62)
. (62) , що є розв’язком оптимізаційної задачі. Підставляючи знайдені значення факторів виробництва у виробничу функцію, отримаємо значення максимального випуску за заданих обмежень на витрати.
, що є розв’язком оптимізаційної задачі. Підставляючи знайдені значення факторів виробництва у виробничу функцію, отримаємо значення максимального випуску за заданих обмежень на витрати.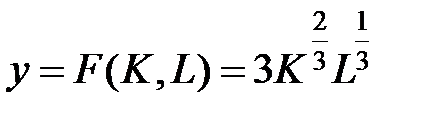 .
.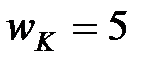 ум.од., ставка заробітної плати
ум.од., ставка заробітної плати 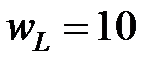 ум. од. Визначити граничну норму заміни одного працівника фондами в оптимальній точці.
ум. од. Визначити граничну норму заміни одного працівника фондами в оптимальній точці.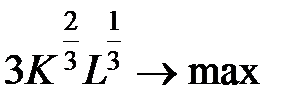
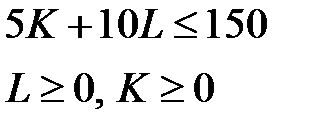 .
.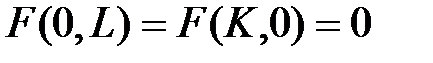 , то в оптимальному розв’язку
, то в оптимальному розв’язку  .
.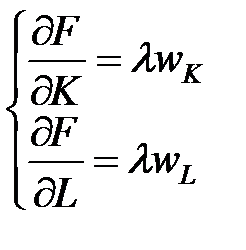
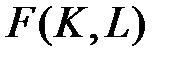 , отримаємо:
, отримаємо: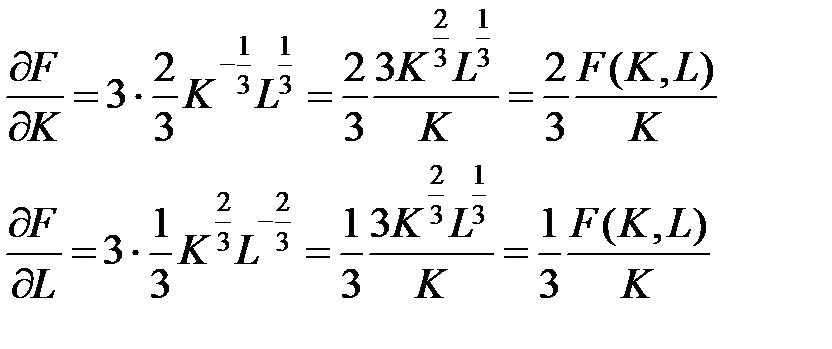
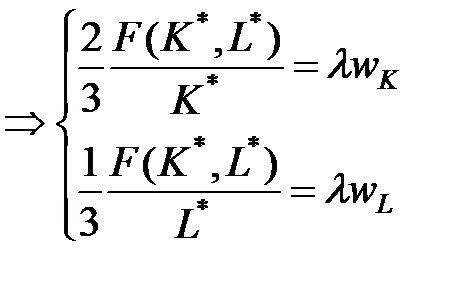
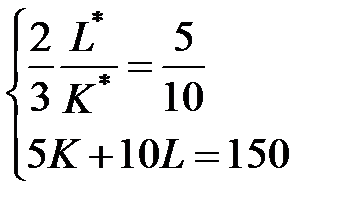 ,
,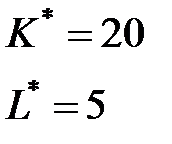
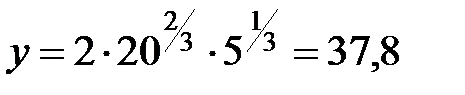 .
.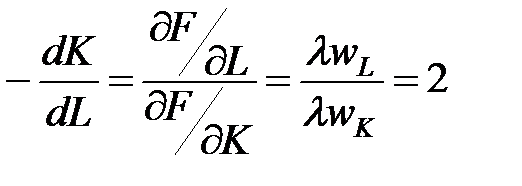 ,
,


