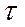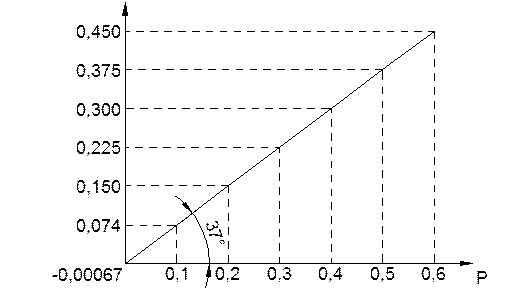Задача №1. Природа грунтов и показатели физико-механических свойств
Расчетно-графическая работа
по курсу: «Механика грунтов»
Выполнил: ____________ студент 4 курса ФЗО спец. ПГС сокр. формы обучения шифр 051514 Лыткин Андрей Николаевич
Проверил: _____________ старший преподаватель Бобров Владимир Владимирович
г. Сыктывкар Оглавление Стр.
Задача №1. Природа грунтов и показатели физико-механических свойств. 3 Задача №2. Напряжения в грунтах от действия внешних сил. 8 Задача №3. Напряжения в грунтах от действия внешних сил. 10 Задача №4. Напряжения в грунтах от действия внешних сил. 15 Задача №5. Теории предельного напряженного состояния грунтов. 21 Задача №6. Теории предельного напряженного состояния грунтов. 24 Задача №7. Деформации грунтов и прогноз осадок фундаментов. 30 Задача №8. Деформации грунтов и прогноз осадок фундаментов. 34 Список использованных источников и литературы.. 37 Задача №1. Природа грунтов и показатели физико-механических свойств По результатам лабораторных исследований свойств грунтов требуется: а) для образцов песчаного грунта построить интегральную кривую гранулометрического состава, определить тип грунта по гранулометрическому составу и степени его неоднородности, дать оценку плотности сложения и степени влажности, определить расчетное сопротивление R 0;
для образцов глинистого грунта определить тип грунта, разновидность по консистенции и расчетное сопротивление R 0;
б) построить график компрессионной зависимости вида
в) построить график сдвига вида
Решение: а) Для определения степени неоднородности гранулометрического состава песчаного грунта построим интегральную кривую гранулометрического состава:
Рис.1-1. Интегральная кривая гранулометрического состава Степень неоднородности гранулометрического состава U определяется по формуле: В нашем случае Величина коэффициента пористости е равна:
По Табл. Б18 ГОСТ 25100-95 песок средней крупности с таким коэффициентом пористости характеризуется как плотный. Разновидность песчаных грунтов по степени водонасыщения S r определяется согласно Табл. Б17 ГОСТ 25100-95.
В соответствии с вышеуказанной таблицей данные пески являются маловлажными. Расчетное сопротивление плотных песков средней крупности Тип глинистого грунта и разновидность по консистенции определяются по заданным границам текучести, раскатывания и природной влажности. Разность между влажностями на границах текучести и раскатывания называется числом (индексом) пластичности и обозначается I p:
По Табл.Б11 ГОСТ 25100-95 данный глинистый грунт можно считать суглинком. Показатель текучести I L определяется по формуле:
В соответствии с Табл. Б14 ГОСТ 25100-95 данный суглинок тугопластичной консистенции. Величина коэффициента пористости е равна:
Расчетное сопротивление тугопластичных суглинков с показателем текучести б) Для построения графика компрессионной зависимости и определения коэффициента относительной сжимаемости грунта необходимо, прежде всего, вычислить коэффициенты пористости грунта e i, соответствующие заданным ступеням нагрузки, по формуле:
где e i – искомое значение коэффициента пористости грунта после уплотнения под нагрузкой Р i; e 0 – начальное (до уплотнения) значение коэффициента пористости грунта; S i – полная осадка образца грунта при заданной нагрузке Р i, измеренная от начала загружения; h – начальная(до уплотнения) высота образца грунта. Рассчитанные коэффициенты пористости грунта e i внесем в таблицу:
Рис.1-2. График компрессионной зависимости Коэффициент относительной сжимаемости грунта m v определяется по формуле:
где m 0 – коэффициент сжимаемости грунта для заданного расчетного интервала давлений:
e 1 и e 2 –коэффициенты пористости, соответствующие давлениям P 1 и P 2; P 2 – P 1 – заданный расчетный интервал давлений, или так называемое действующее давление. Коэффициент относительной сжимаемости грунта m v равен:
что свидетельствует о том, что грунт – среднесжимаемый. Модуль деформации вычисляют для заданного расчетного интервала давлений по формуле:
в) Для определения нормативного значения угла внутреннего трения грунта Для начала построим вспомогательную таблицу для нахождения искомых величин методом наименьших квадратов:
Используя рассчитанные значения, находим:
Строим график сдвига
Рис.1-3. График сдвига
|

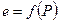 , определить для заданного расчетного интервала давлений коэффициент относительной сжимаемости грунта, модуль деформации грунта и охарактеризовать степень сжимаемости грунта (начальная высота образца грунта h = 20 мм);
, определить для заданного расчетного интервала давлений коэффициент относительной сжимаемости грунта, модуль деформации грунта и охарактеризовать степень сжимаемости грунта (начальная высота образца грунта h = 20 мм);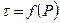 , методом наименьших квадратов определить нормативное значение угла внутреннего трения
, методом наименьших квадратов определить нормативное значение угла внутреннего трения 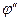 и сцепление
и сцепление 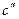 грунта.
грунта.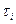 , МПа, при нормальном удельном давлении, передаваемом на образце грунта Pi, МПа
, МПа, при нормальном удельном давлении, передаваемом на образце грунта Pi, МПа
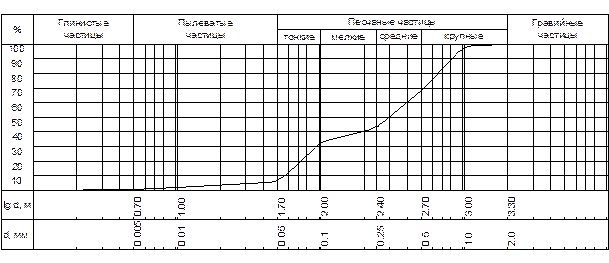
 где d 60, d 10 – диаметры частиц, меньше которых в данном грунте содержится соответственно 60 и 10% частиц по массе (принимается по интегральной кривой гранулометрического состава грунта).
где d 60, d 10 – диаметры частиц, меньше которых в данном грунте содержится соответственно 60 и 10% частиц по массе (принимается по интегральной кривой гранулометрического состава грунта).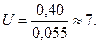 Таким образом, можно сделать вывод, что песок неоднородный. Данный песчаный грунт относится к пескам средней крупности согласно Табл. Б10 ГОСТ 25100-95.
Таким образом, можно сделать вывод, что песок неоднородный. Данный песчаный грунт относится к пескам средней крупности согласно Табл. Б10 ГОСТ 25100-95.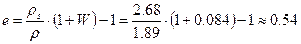 .
.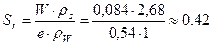 .
.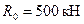 .
.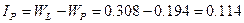
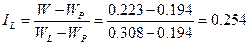
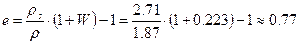 .
.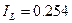 и коэффициентом пористости
и коэффициентом пористости 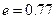 будет равным
будет равным 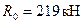 .
.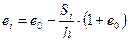
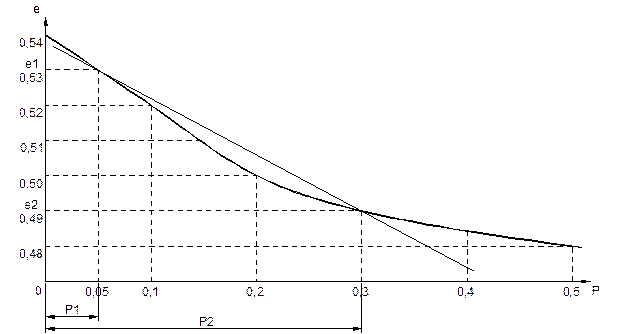
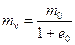 ,
,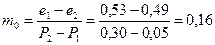
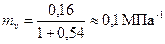 ,
,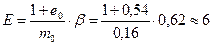 .
.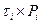
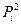
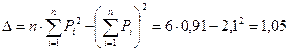
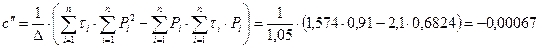
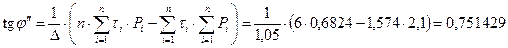
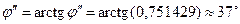 .
.