Задача №3. Напряжения в грунтах от действия внешних сил
Исходные данные: Горизонтальная поверхность массива грунта по прямоугольным плитам с размерами в плане 260×210 и 500×240 (размеры в сантиметрах) нагружена равномерно распределенной вертикальной нагрузкой интенсивностью 0,34 МПа и 0,38 МПа соответственно. Определить величины вертикальных составляющих напряжений σ;Z от совместного действия внешних нагрузок в точках массива грунта для заданной вертикали, проходящей через одну из точек М1, М2, М3 на плите №1. Расстояние между осями плит нагружения – 300 см. Точки по вертикали расположить от поверхности на расстоянии 100, 200, 400, 600 см. По вычисленным напряжениям построить эпюры распределения σ;Z (от каждой нагрузки отдельно и суммарную).
Рис. 3-1. Расчетная схема Решение: Используя метод угловых точек определение вертикальных составляющих напряжений в точке проводится по формуле: Для площадок под центром загружения прямоугольника: Для площадок под углом загруженного прямоугольника: 1. Рассмотрим плиту №1. а) Определим величину вертикальных составляющих напряжений в точке М1. Разделим плиту на две составляющие таким образом, чтобы М1 являлась углом длинной стороны прямоугольников. Получатся два зеркально отраженных прямоугольника со сторонами: Для глубины 100 см: Для глубины 200 см: Для глубины 400 см: Для глубины 600 см: б) Определим величину вертикальных составляющих напряжений в точке М2. Поскольку М2 находится под центром плиты, применяем формулы для центра загружения: Для глубины 100 см: Для глубины 200 см: Для глубины 400 см: Для глубины 600 см: в) Определим величину вертикальных составляющих напряжений в точке М3. Для глубины 100 см: Для глубины 200 см: Для глубины 400 см: Для глубины 600 см: 2. Рассмотрим плиту №2 Поскольку точки М находятся вне прямоугольника давлений, величина
а) Определим величину вертикальных составляющих напряжений в точке М1. Разделим плиту на две составляющие таким образом, чтобы М1 являлась углом длинной стороны прямоугольников. Получатся два зеркально отраженных прямоугольника со сторонами: Для глубины 100 см: Для глубины 200 см: Для глубины 400 см: Для глубины 600 см: б) Определим величину вертикальных составляющих напряжений в точке М2. Разделим плиту на две составляющие таким образом, чтобы М2 являлась углом длинной стороны прямоугольников. Получатся два зеркально отраженных прямоугольника со сторонами: Для глубины 100 см: Для глубины 200 см: Для глубины 400 см: Для глубины 600 см: в) Определим величину вертикальных составляющих напряжений в точке М3. Разделим плиту на две составляющие таким образом, чтобы М3 являлась углом длинной стороны прямоугольников. Получатся два прямоугольника, причем верхний со сторонами: Для глубины 100 см: Для глубины 200 см: Для глубины 400 см: Для глубины 600 см: 3. Пользуясь принципом независимости действия сил, находим алгебраическим суммированием напряжения в заданных точках массива грунта. Для действия распределенной нагрузки Р 1:
Для действия распределенной нагрузки Р 2:
Для действия суммарной нагрузки:
4. На основании проведенных расчетов строим эпюры распределения σ;Z.
Рис. 3-2. Эпюры распределения вертикальных напряжений σ;Z
|

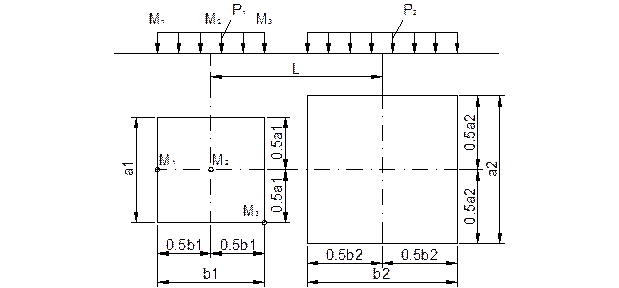
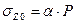 , где α; – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения
, где α; – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения  (а – длинная ее сторона, b – ее ширина) и отношения
(а – длинная ее сторона, b – ее ширина) и отношения  (z – глубина, на которой определяется напряжение
(z – глубина, на которой определяется напряжение  ), P – интенсивность равномерно распределенной нагрузки.
), P – интенсивность равномерно распределенной нагрузки.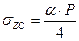 , где α; – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения
, где α; – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения 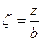 (z – глубина, на которой определяется напряжение
(z – глубина, на которой определяется напряжение  ), P – интенсивность равномерно распределенной нагрузки.
), P – интенсивность равномерно распределенной нагрузки. см,
см, 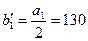 см.
см. МПа
МПа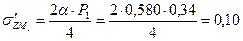 МПа
МПа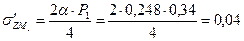 МПа
МПа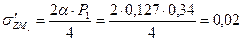 МПа
МПа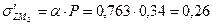 МПа
МПа МПа
МПа МПа
МПа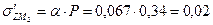 МПа
МПа МПа
МПа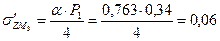 МПа
МПа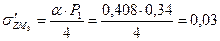 МПа
МПа МПа
МПа .
.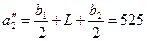 см,
см,  см.
см.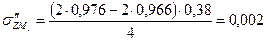 МПа
МПа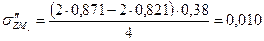 МПа
МПа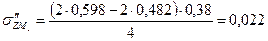 МПа
МПа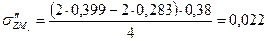 МПа
МПа см,
см, 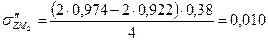 МПа
МПа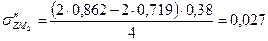 МПа
МПа МПа
МПа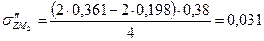 МПа
МПа см,
см, 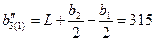 см; нижний –
см; нижний –  см,
см, 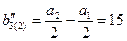 см.
см. МПа
МПа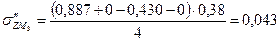 МПа
МПа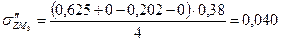 МПа
МПа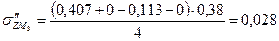 МПа
МПа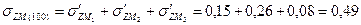 МПа
МПа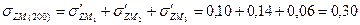 МПа
МПа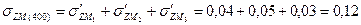 МПа
МПа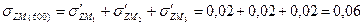 МПа
МПа МПа
МПа МПа
МПа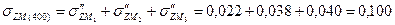 МПа
МПа МПа
МПа МПа
МПа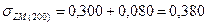 МПа
МПа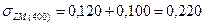 МПа
МПа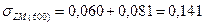 МПа
МПа



