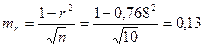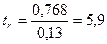Корреляция. При одновременном изучении совокупности по нескольким признакам нередко обнаруживается, что между признаками существует связь
При одновременном изучении совокупности по нескольким признакам нередко обнаруживается, что между признаками существует связь. Взаимная связь признаков, при которой значение одного признака соответствует значению другого признака или при изменении одного признака второй тоже изменяется, называется корреляцией. По форме корреляция бывает прямолинейной (между суточным удоем и удоем за лактацию) и криволинейной (между живой массой и удоем за лактацию). По направлению корреляция может быть положительной и отрицательной. При положительной корреляции с увеличением одного признака второй тоже увеличивается (суточный удой и удой за лактацию, живая масса и удой, складчатость кожи у овец и настриг шерсти). При отрицательной корреляции увеличение одного признака ведет к снижению другого (удой и жирность молока, плодовитость у свиней и масса поросят при рождении, яйценоскость и масса яйца, длина туловища и толщина шпика). По сочетанию удоя и содержания жира в молоке профессор Соловьев выделил 4 типа животных: 1. Животные, у которых с повышением удоя содержание жира увеличивается. Это самый желательный тип. 2. Животные, у которых с повышением удоя содержание жира остается на одном уровне. 3. Животные, у которых с повышением удоя содержание жира снижается. 4. Животные, у которых с понижением удоя содержание жира увеличивается. Для оценки силы и направления взаимосвязи между признаками вычисляют коэффициент корреляции (r). Значение коэффициента корреляции находятся в пределах от -1 до +1. Если r=0, то корреляция отсутствует; r=-1 – полная отрицательная корреляция; r=+1 – полная положительная корреляция. Если r<0,3 – корреляция слабая, низкая; r=0,3-0,7 – корреляция средняя; r>0,7 – корреляция высокая, сильная. Коэффициент корреляции для большой выборки вычисляется путем построения корреляционной решетки. Рассмотрим вычисление коэффициента корреляции на примере. Вычисление коэффициента корреляции между живой массой и обхватом груди у свиноматок 1. Исходя из лимитов, определяем классовый промежуток, начало и конец каждого класса по вариационному ряду Х (обхват груди) и ряду У (живая масса). 2. Распределяем свиноматок по класса корреляционной решетки с учетом живой массы (У) и обхвата груди (Х), т.е. точкуем. 3. По каждому вариационному ряду проставляем количество вариант в каждом классе (Рх и Ру). 4. По каждому вариационному ряду выделяем модальные классы и находим отклонения ах и ау. 5. Вычисляем Рх×ах; Рх×ах2; Ру×ау; Ру×ау2 и их суммы. Таблица 2 – Корреляционная решетка
6. Вычисляем коэффициент корреляции по формуле
где bx и by – поправки к модальным классам; n – количество животных (в нашем примере n=400); σх и σу – среднее квадратическое отклонение по ряду Х и ряду У, вычисленное без умножения на шаг; ∑Рахау – сумма произведений количества вариант в каждой клетке на отклонение ах и ау. n=400 голов
Чтобы найти сумму Рахау, нужно для каждой клетки найти произведение количества вариант на ах и ау. Для первой клетки это будет выглядеть так: 2×(-3)×(-3)=18, запишем в виде степени. И так далее для каждой клетки корреляционной решетки, где есть варианты. Затем найдем сумму Рахау по четырем квадратам и запишем в правом нижнем углу корреляционной решетки. ∑Рахау=144-7-3+772=906
Таким образом, между живой массой и обхватом груди у свиноматок нами выявлена сильная положительная корреляция. Ошибку и критерий достоверности для коэффициента корреляции находим по следующим формулам:
mr=0,016 tr=51 Вычисление коэффициента корреляции для малой выборки Пример: Вычислить коэффициент корреляции между концентрацией спермиев (Х) и содержанием липоидного фосфора (У) в эякуляте у 10 быков. Для этого построим таблицу и занесем в нее по каждому из быков значение Х и У:
ах, ау – отклонение каждой варианты по ряду Х и ряду У от средней арифметической (ах= Х i- σх, σу – среднее квадратическое отклонение по признаку Х и У, вычисленное по формуле для малой выборки, т.к. n=10.
Коэффициент корреляции находим по формуле:
Между концентрацией спермиев и содержанием липоидного фосфора нами выявлена высокая положительная корреляция.
|

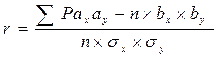 (21)
(21)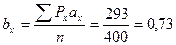

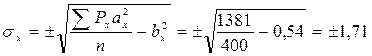
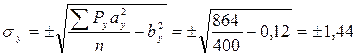
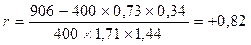
 (22)
(22)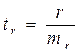 (23)
(23)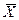 ; ау= У i-
; ау= У i- 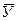 ).
).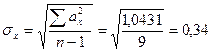

 (24)
(24)