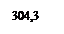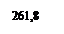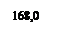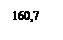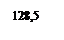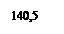Эмпирические и теоретические линии регрессии, их построение
Если коэффициент регрессии показывает на сколько изменяется величина одного признака при изменении другого на единицу измерения, то линии регрессии позволяют установить по любому значению одного признака значение другого признака. Линии регрессии бывают эмпирические и теоретические. Эмпирические линии – это ломаные линии характерные для данной выборки на момент исследования. Теоретические линии – это прямые линии, полученные в результате сглаживания ломаных линий, и показывают возможные изменения популяции во времени. Для построения эмпирических линий регрессии необходимо: 1. Построить новую корреляционную решетку. 2. Заменить начало и конец каждого класса средним значением ((начало+конец)/2, например (152+171)/2=161,5) 3. Перенести со старой решетки значение вариант. 4. Выделить модальные классы. 5. Найти для каждого класса по обхвату груди Х среднее значение живой массы У (через среднюю взвешенную). Для первого класса средняя живая масса будет равна:
Средняя живая масса для первого класса = 2×161,5+3×181,5+1×201,5/6=178,1 кг по обхвату груди
6. Аналогично находят для каждого класса по живой массе У среднее значение Х по обхвату груди. 7. Заполнить таблицы средних значений для построения ломаных линий: Для линии У от Х:
Для линии Х от У:
7. Вычислить координаты точки пересечения эмпирических линий, координатами ее будут средние арифметические по Х и У.
Ах= 138+3=141 l х=6 bх=0,73
Ау=212+10=222
Точка пересечения эмпирических линий – С (145,4;228,6)
Построение теоретических линий регрессии: 1. Находим координаты точек для построения прямых линий, исходя из уравнений прямолинейной регрессии: Хi- Уi- 2. Преобразуем первое уравнение (формула 32): ХI= Rx/y× (Уi- Rx/y=0,29 3. Определяем Х1 при У1. За У1 можно взять начало первого класса по У, если количество вариант в этом классе больше или равно 3. Х1=0,29× (152-228,6)+145,4=123 Х1=123 при У1=152 4. За У2 берем начало последнего класса по У, если n≥3. Х2=0,29× (312-228,6)+145,4=169,7 Х2=169,7 при У2=312 5. Преобразуем второе уравнение (формула 33): Уi= Rу\х× (Хi- Rу\х=2,29 6. За Х1 берем начало первого класса по Х, если n≥3. У1=2,29× (120-145,4)+228,6=170,6 У1=170,6 при Х1=120 7. За Х2 берем начало последнего класса по Х, если n≥3. У2=2,29× (174-145,4)+228,6=294,2 У2=294,2 при Х2=174
|


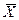 =141+0,73×6=145,4 см
=141+0,73×6=145,4 см
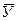 =222+0,34×20=228,6 кг
=222+0,34×20=228,6 кг