Сведения, об использованных методах измерения
Федеральное агентство связи ГОУ ВПО Сибирский государственный университет Телекоммуникаций и информатики Кафедра ПДС и М
Лабораторная работа № 1.4
Упрощенная процедура обработки результатов прямых измерений с многократными наблюдениями
Выполнил: ст.гр. М-91 Гусинский Р.Е. Проверил: преподаватель Квиткова И.Г
Новосибирск 2012 г.
1. Цель работы. Ознакомление с упрощенной процедурой обработки результатов прямых измерений с многократными наблюдениями. Получение, применительно к упрощенной процедуре, навыков обработки результатов наблюдений, оценки погрешностей результатов измерений. Программа лабораторной работы. 2.1.Выполнить независимые многократные наблюдения в автоматическом режиме. 2.2.Произвести автоматизированную упрощенную процедуру обработки результатов независимых многократных наблюдений. 2.3.Оформить полученные результаты в отчете. 2.4.Провести анализ и сделать выводы по работе. Сведения, об использованных методах измерения Для обработки результатов многократных наблюдений могут быть использованы различные процедуры. Стандартная методика весьма трудоемка, причем, далеко не всегда можно выполнить серию наблюдений, объем которой достаточен для выявления закона распределения случайной составляющей погрешности и применения стандартной методики. Кроме того, если неисключенный остаток систематической погрешности сравнительно велик, выполнение длинной серии наблюдений для максимального уменьшения влияния случайной составляющей погрешности теряет смысл. Упрощенная процедура обработки результатов прямых измерений с многократными наблюдениями применяется, если число наблюдений n≤30. При использовании этой процедуры за результат измерения также как и всегда принимают среднее арифметическоезначение результатов исправленного ряда наблюдений, которое вычисляют по формуле:
среднее арифметическое значение исправленного ряда наблюдений, n – количество результатов наблюдений. Затем вычисляют оценку СКО результата наблюденийS по формуле:
Эта величина является приближенной оценкой среднего квадратического отклонения σ; – параметра нормального закона распределения. Чем больше наблюдений проведено, тем точнее эта оценка. Для расчета оценки среднего квадратического отклонения результатаизмерения
Оценка среднего квадратического отклонения Для нахождения границ доверительного интерваласлучайной составляющей погрешности результата измерений
где t – квантиль распределения Стьюдента, определенный для доверительной вероятности Часто имеет место ситуация, когда на результат измерений оказывают влияние две составляющие, а именно: погрешность средства измерений
где Если доверительная вероятность для границ погрешности средства измерений не указана, то при расчетах ее можно принимать равной Из формулы 3 видно, что по мере того, как количество наблюдений растет, вклад случайной составляющей погрешности в окончательный результат постепенно уменьшается и может настать момент, когда вклад случайной погрешности в общую погрешность измерений станет пренебрежимо мал. Ясно, что в этом случае дальнейшее увеличение количества наблюдений бессмысленно. Таким образом, измерения с многократными наблюдениями оправданы не всегда, а при их планировании полезно заранее оценить требуемый объем выборки. В противном случае трудоемкость измерений может оказаться неоправданно высокой, а увеличение точности - незначительным.
|

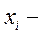
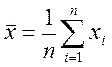 (1)
(1) где – i -й исправленный результат наблюдения,
где – i -й исправленный результат наблюдения,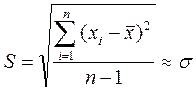 (2)
(2)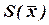 используют формулу:
используют формулу: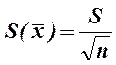 (3)
(3) является основной характеристикой случайной составляющей погрешности результата измерений.
является основной характеристикой случайной составляющей погрешности результата измерений. в рассматриваемом случае необходимо проанализировать априорную информацию об объекте измерений и условиях проведения измерений. Если явно выраженных причин, способных привести к отклонению закона распределения результатов наблюдений от нормального, не выявлено, то доверительные границы случайной составляющей погрешности результата измерения находят с помощью квантилей распределения Стьюдента по формуле:
в рассматриваемом случае необходимо проанализировать априорную информацию об объекте измерений и условиях проведения измерений. Если явно выраженных причин, способных привести к отклонению закона распределения результатов наблюдений от нормального, не выявлено, то доверительные границы случайной составляющей погрешности результата измерения находят с помощью квантилей распределения Стьюдента по формуле: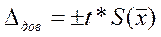 , (4)
, (4) .
.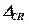 (инструментальная погрешность) и случайная составляющая погрешности
(инструментальная погрешность) и случайная составляющая погрешности 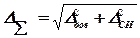 , (5)
, (5)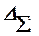 – граница результирующей абсолютной погрешности,
– граница результирующей абсолютной погрешности,  и
и 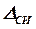 – границы отдельных составляющих абсолютных погрешностей, причем, если модуль одной из составляющих превышает модуль другой составляющей более чем в 8 раз, то влиянием меньшей составляющей на результирующую погрешность можно пренебречь.
– границы отдельных составляющих абсолютных погрешностей, причем, если модуль одной из составляющих превышает модуль другой составляющей более чем в 8 раз, то влиянием меньшей составляющей на результирующую погрешность можно пренебречь. (МИ 1552-86). Результат измерений представляют в виде:
(МИ 1552-86). Результат измерений представляют в виде:  , условия измерений; при этом числовое значение результата измерений должно оканчиваться цифрой того же разряда, что и округлённое значение границы абсолютной погрешности
, условия измерений; при этом числовое значение результата измерений должно оканчиваться цифрой того же разряда, что и округлённое значение границы абсолютной погрешности  .
.


