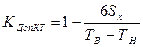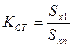Анализ формы гистограммы
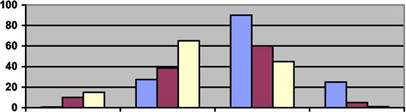
Если гистограмма симметрична относительно номинального значения m0 с явным убыванием от цента к краям распределения, то можно предположить, что закон распределения погрешностей нормальный. При этом, если ±3Sx ≤ (Tв-Тн), то данный процесс признается удовлетворительным (точным и стабильным). На рисунке 1 представлена такая гистограмма.
Рисунок 1 На рисунке 2 представлена гистограмма частот, по характеру которой (плосковершинность) можно предположить, что распределение суммарной погрешности представляет собой композицию двух распределений: нормального (распределение случайных погрешностей) и равной вероятностей (распределение переменных систематических погрешностей).
Рисунок 2
Рисунок 3 На рисунке 3 изображено островершинное распределение, которое возникает вследствие изменчивости рассеяния. Островершинность бывает тем больше, чем больше предел изменения Sx. Факторы, влияющие на появление таких распределений, это износ инструмента (притупление), вызывающих увеличение силы резания, а следовательно, и увеличение упругих деформаций узлов станка; периодические колебания режима работы оборудования и др.
Рисунок 4 На рисунке 4 представлена диаграмма с левосторонней асимметрией, возникающей при контроле изделий, имеющих овальность, эксцентриситет, шероховатость.
Рисунок 5 Распределение с правосторонней асимметрией (рис. 4) появляются при смещении центров настройки по параболе (суммарное воздействие размерного износа инструмента и температурного изменения). Однако по виду гистограммы можно сделать безошибочные выводы. Для более точного решения поставленной задачи необходимо провести проверку статистической гипотезы: если гипотеза о нормальности закона распределения не подтверждается, оценивание ведут на основе того распределения, которое подтверждается, либо, что бывает чаще, получают приближенную оценку зоны рассеяния; при подтверждении гипотезы о соответствии эмпирического распределения нормальному закону распределения определяют коэффициент точности изготовления изделия заданным размерам, как отношение поля рассеяния к полю допуска, сформулированного в НТД. Стандартные показатели: Коэффициент точности Кт определяется по формуле:
(2.1) где 6Sx - поле рассеяния, в которое укладывается 99,75% значений случайной величины при нормальном распределении полученных в процессе контроля; (Тв-Тн) - ширина поля допуска, заданная в НТД. Коэффициент точности настройки процесса:
(2.2) где Ен - значение смещения вершины кривой распределения случайной величины от середины поля допуска m0; m1 -значение, соответствующее вершине гистограммы. Фактический коэффициент точности настройки определяют по выражению:
(2.3) где X - среднее значение выборки. Допустимый коэффициент точности настройки определяют по выражению:
Запас точности Кз.т. является резервом на смещение наладки и смещение ее при последующей длительной эксплуатации. Коэффициент запаса точности определяется по формуле:
(2.5) Коэффициент стабильности технологического процесса Кст определяется по формуле:
где Sx1 - среднее квадратическое отклонение в фиксированный момент времени; Sxn - среднее квадратическое отклонение в сравниваемый момент времени.
Вероятность появления бракованных изделий, которые выпускает стабильная технологическая система, определяется по формуле:
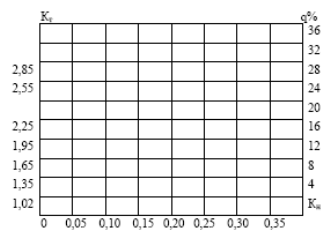
где F(u) - интегральная функция распределения вероятности нормированной случайной величины u; Тн и Тв - верхняя и нижняя границы поля допуска; m0 - номинальное значение случайной величины Х, совпадающее с серединой поля допуска; σх - генеральное среднее квадратическое отклонение (если оно известно). Если известны коэффициенты точности и настроенности, то уровень дефектности можно определить также следующей номограмме, изображенной на рисунке 6:
Рисунок 6 Правило принятия решения:
Рисунок 7
Рисунок 8 При Кт<1 технологический процесс с вероятностью р=0,9975 можно считать обеспечивающим более высокую точность, чем требует НТД, то есть качество продукции можно считать хорошим. При Кт=1 качество продукции среднее. При Кт>1 технологический процесс, очевидно, не обеспечивает заданного допуска изделий, поэтому будет реальной вероятность появления брака, то есть качество продукции можно считать низким.
На рисунке 7 показаны графики распределения вероятностей случайной величины при различных коэффициентах точности. На рисунке 8 показан график распределения вероятности случайной величины со смещением вершины кривой распределения от середины поля допуска. Таким образом, технологический процесс полностью обеспечивает точность, т.е. соответствие НТД качества выпускаемой продукции, если выполняются следующие условия:
|