Шахматный ферзь

Создайте loft-модель, взяв в качестве пути линию, а в качестве сечения — окружность (рис. 16). Вы получите ничем не примечательный цилиндр (рис. 17), который путем очень простых манипуляций масштабирования можно превратить в самые разные модели, например в шахматного ферзя. Перейдите в режим редактирования loft-объекта, разверните свиток Deformation (Деформация) и щелкните на кнопке Scale. На первом этапе добавьте в окне Scale Deformation порядка 8-10 управляющих точек (рис. 18) — зачастую на начальном этапе построения той или иной модели точное число дополнительных вершин определить сложно, но ничего страшного здесь нет, ведь ситуацию в любой момент можно скорректировать, добавив недостающие вершины или удалив те, что оказались лишними. Затем начните по очереди перемещать вершины, внимательно наблюдая за объектом в окне Perspective. В конечном счете кривая деформации станет напоминать кривую на рис. 19, а внешний вид модели — рис. 20. В целом полученный loft-объект действительно напоминает шахматную фигуру, но у реального ферзя, как правило, средняя часть фигуры (рис. 21) имеет не прямолинейную, а криволинейную поверхность. Поэтому необходимо конвертировать отвечающую за данную область управляющую вершину в тип Bezier-Smooth, а затем отрегулировать степень искривления поверхности (рис. 22). Окончательный вид ферзя представлен на рис. 23.

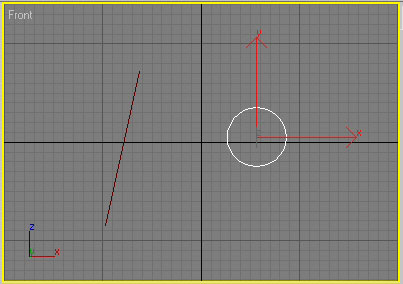
Рис. 16. Исходные элементы loft-объекта

Рис. 17. Начальный вид loft-объекта

Рис. 18. Окно Scale Deformation после создания дополнительных вершин

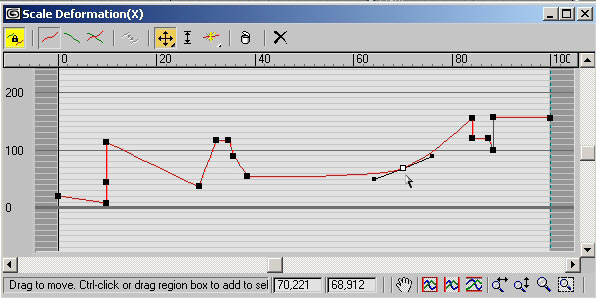
Рис. 19. Окно Scale Deformation после размещения новых вершин

Рис. 20. Loft-объект после грубого масштабирования

Рис. 21. Loft-объект с указанием области криволинейной поверхности

Рис. 22. Окончательный вид кривой деформации

Рис. 23. Ферзь