Определение синуса, косинуса, тангенса и котангенса
I. Вычисление элементов прямоугольного треугольника При выполнении заданий 7 на вычисление элементов прямоугольного треугольника достаточно знать определение синуса, косинуса и тангенса острого угла прямоугольного треугольника, основное тригонометрическое тождество и теорему Пифагора.
Пифагоровы треугольники: 3,4,5; 5,12,13; 8,15,17; 7,24,25. Определение синуса, косинуса, тангенса и котангенса острого угла: sinA = АС Основное тригонометрическое тождество: sin²A+ cos²A=1
sin(180˚- α) = sinα; cos(180˚-α) = -cosα
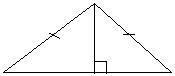
Нвершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. А С СН= 3) В ∆АВС - равнобедренный, ∆АВН=∆ВСН АС ВН - медиана, биссектриса, высота. Н
Решать задания 7 можно по-разному. Показано несколько образцов решения задач.
|
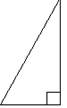1) В Теорема Пифагора: АВ² = АС² + ВС².
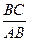; cosA= 
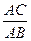; tgA = 
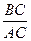; ctgA =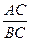 
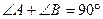Формулы приведения: sin(90˚- α) = cosα; cos(90˚-α) = sinα
)
)
)
)
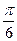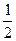
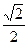
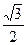
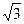
2) В Высота прямоугольного треугольника, проведенная из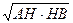
; АС = 
