Основные теоретические положения. Обратная задача моделирования
Обратная задача моделирования. Метод наименьших квадратов. Рассмотрим динамическую систему, модель которой представляется функциональной зависимостью Прямая задача моделирования: пусть сигнал управления Необходимо определить значение выхода
Рис. 1 Структурная схема задачи прямого моделирования Обратная задача моделирования (идентификация): известно значение сигнала управления Необходимо определить вид функции Одним из распространенных методов идентификации динамических систем является метод наименьших квадратов (МНК).
Рис. 2 Структурная схема идентификации Рассмотрим линейную динамическую систему, заданную дифференциальным уравнением (иначе - в виде передаточной функции):
здесь
Перепишем это уравнение, оставляя в левой части выходной сигнал
иначе:
где введены следующие обозначения: По-сути мы получили модель в виде При решении задачи параметрической идентификации, параметры модели (1) (и соответственно (2)) являются неизвестными и подлежащими определению. Пусть сигнал
Данная запись означает, что минимальное отклонение (по квадратичному критерию) измеряемого выхода Для поиска минимума критерия находим его производную по вектору
Результатом минимизации данного критерия будет система алгебраических уравнений вида:
или в матричном виде:
Тем самым решение задачи идентификации по схеме МНК будет получаться на основе решения системы уравнений (3), которое дает искомые оценки вектора параметров
где Приведение модели системы к линейно-регрессионному виду. Для использования схемы МНК необходимо уравнение модели привести к линейно-регрессионному виду (2): Необходимо отметить, что такое приведение всегда неоднозначно (может быть получено множеством способов). Отметим некоторые особенности построения схемы МНК: 1) Приведение модели к линейно-регрессионному виду всегда начинается с составления уравнения модели, включающего только измеряемые переменные. В этом уравнении производится группировка относительно переменных, после чего выбирается выходная переменная Пример: в уравнении После группировки получаем 2) Знаки регрессионных переменных Пример: пусть 3) В левой части линейно-регрессионного уравнения, в качестве выходной переменной Пример: Вариант 1: в качестве выходной переменной берем исходную Вариант 2: в качестве выходной переменной берем производную Выбор выходной переменной влияет на вид регрессионного уравнения и может влиять на надежность и точность результатов схем МНК-идентификации, построенной по этому уравнению. 4) Одно из основных условий, обеспечивающих работоспособность схемы МНК-идентификации, является использование данных о динамике процессов при формировании расчетной выборки (матриц Пример: Задано уравнение
Вариант 1: пусть Вариант 2: пусть
5) При численном моделировании исходной системы (т.е. в дискретном времени
|

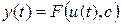 , где
, где 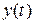 - выходной (измеряемый) сигнал,
- выходной (измеряемый) сигнал, 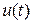 - входная управляющая переменная,
- входная управляющая переменная,  - совокупность параметров модели.
- совокупность параметров модели. , известна функция модели
, известна функция модели 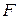 и определенны ее параметры
и определенны ее параметры  на указанном периоде времени при заданных начальных условиях (н.у.) выходной функции
на указанном периоде времени при заданных начальных условиях (н.у.) выходной функции  и ее производных (если потребуется).
и ее производных (если потребуется).
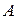 параметров модели
параметров модели  на основе данных измерений входного
на основе данных измерений входного 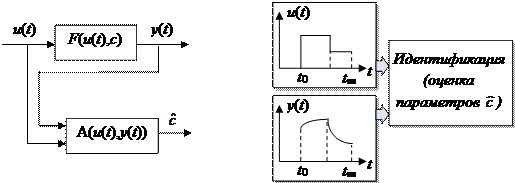
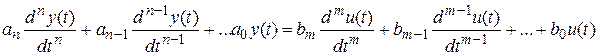 (1)
(1) ,
,  - параметры системы,
- параметры системы,  ,
, 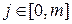 . Вводя обозначение для оператора дифференцирования
. Вводя обозначение для оператора дифференцирования  , уравнение (1) можно записать в виде:
, уравнение (1) можно записать в виде: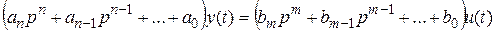

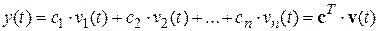 (2)
(2) ,
, 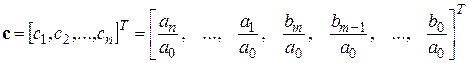 - вектор параметров,
- вектор параметров, 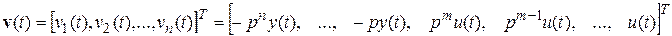 - вектор регрессионных переменных
- вектор регрессионных переменных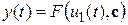 , при этом параметры описываются вектором
, при этом параметры описываются вектором  , а функция
, а функция 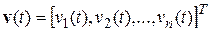 - доступны к измерению (известны) на периоде
- доступны к измерению (известны) на периоде  . Будем искать оценку параметров
. Будем искать оценку параметров  . Для этого построим оценку выхода модели (2) с использованием оценки параметров
. Для этого построим оценку выхода модели (2) с использованием оценки параметров 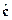 и измеряемых регрессоров
и измеряемых регрессоров 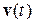 :
:  . Запишем квадратичное уравнение невязки и будем искать его минимум:
. Запишем квадратичное уравнение невязки и будем искать его минимум: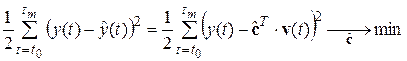
 для всех значений времени
для всех значений времени  достигается при точных оценках параметров
достигается при точных оценках параметров  .
.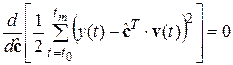
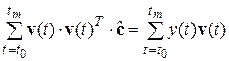
 (3) где
(3) где  (
(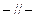 означает запись симметричного относительно диагонали элемента).
означает запись симметричного относительно диагонали элемента). .
.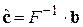 , (4)
, (4)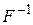 - обратная матрица к
- обратная матрица к 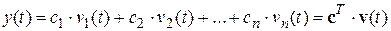

 . Выбираем в качестве выходной переменную
. Выбираем в качестве выходной переменную 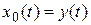 :
: 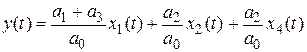 . Заметим, что в этом уравнении можно сгруппировать два последних слагаемых относительно общего параметра
. Заметим, что в этом уравнении можно сгруппировать два последних слагаемых относительно общего параметра  :
: 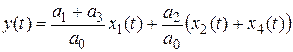 . Вектор регрессоров в правой части запишется в виде:
. Вектор регрессоров в правой части запишется в виде:  ,
, 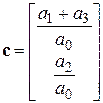 ,
, 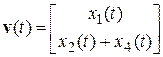 .
. переносятся в вектор
переносятся в вектор  , тогда
, тогда 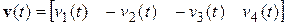 .
.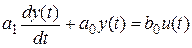 или в операторном виде:
или в операторном виде: 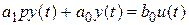
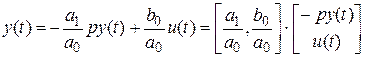
 , тогда
, тогда 
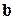 ). Т.е. входное воздействие
). Т.е. входное воздействие 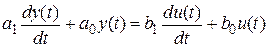 или в операторном виде:
или в операторном виде:  . В качестве выхода берем переменную
. В качестве выхода берем переменную 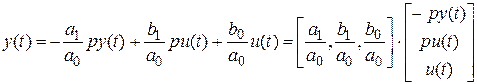
 , отсюда
, отсюда 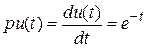 - все регрессионные переменные изменяются со временем («подвижны»).
- все регрессионные переменные изменяются со временем («подвижны»). , отсюда
, отсюда 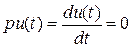 - одна из регрессионных переменных «неподвижна», поэтому ее необходимо исключить из регрессионного уравнения:
- одна из регрессионных переменных «неподвижна», поэтому ее необходимо исключить из регрессионного уравнения: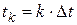 ), вместо непрерывных регрессионных переменных
), вместо непрерывных регрессионных переменных 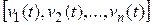 и выходной переменной
и выходной переменной  и
и 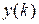 .
.


