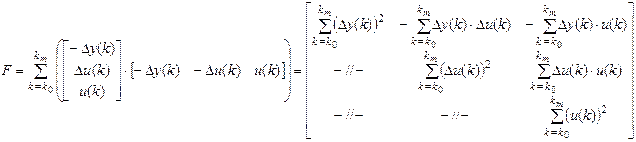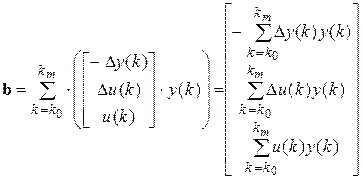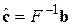Для модели в форме передаточной функции (линейного дифференциального уравнения)1. Моделирование переходного процесса 1) Рассмотрим модель в виде п.ф.:
Зададим временной период 2) Модель переводится в дискретный вид:
где 3) Задается сигнал управления 4) Уравнение модели записывается в регрессионном виде, при этом за выходную переменную принимаем
Раскрывая скобки и группируя переменные, получим:
По этому уравнению строится численная схема расчета переходного процесса (выходного сигнала 2. Идентификация по схеме МНК 1) Еще раз записываем исходное уравнение п.ф. (в дискретной форме):
Выбираем переменную, которая будет служить в качестве выходной в схеме МНК:
2) Полученное линейно-регрессионное уравнение записываем в векторном виде:
где 3) Формируем матрицу Находим решение схемы МНК – оценку вектора параметров по уравнению:
|
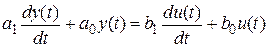
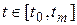и шаг интегрирования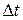 
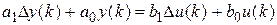
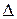- символ оператора дискретного аналога производной (конечная разность), при этом временной интервал разбивается на массив точек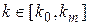 
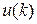и его производная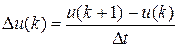 
:
,
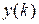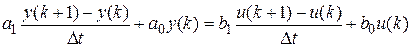
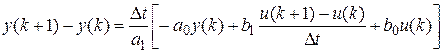
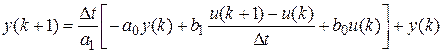
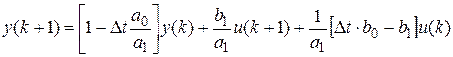
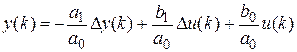
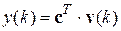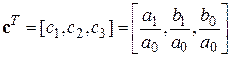- вектор параметров, 
- вектор регрессионных переменных.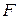
и вектор 
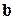для схемы МНК: 
