Определение моментов инерции относительно центральных осей фигуры.
Сначала определим осевые и центробежный моменты инерции относительно собственных главных центральных осей каждого элемента сечения, согласно Приложения: 1) квадрат:
2) четверть круга:
Вычислим координаты центров тяжести сечений каждого элемента относительно центральных осей 1) квадрат:
2) четверть круга:
Полученные значения координат проставляем на чертеже (рис. 5). Определим значение статических моментов площади сечения всей заданной фигуры относительно центральных осей
Полученные значения статических моментов Вычислим значения моментов инерции отдельно взятых элементов сечения относительно центральных осей 1) квадрат:
2) четверть круга:
Моменты инерции всего сечения относительно центральных осей
Проверим правильность нахождения значений моментов инерции площади заданной фигуры относительно центральных осей. Для этого определим значения 1) квадрат:
2) четверть круга:
Для всего сечения будем иметь:
Вычислим по формуле параллельного переноса осей моменты инерции площади заданной фигуры относительно центральных осей
Нетрудно заметить, что полученные значения моментов инерции площади заданной фигуры относительно центральных осей Окончательно принимаем следующие значения: · осевой момент инерции относительно центральной оси
· осевой момент инерции относительно центральной оси
· центробежный момент инерции относительно центральных осей
|

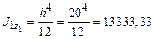 см4;
см4;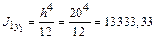 см4;
см4;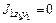 ;
;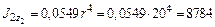 см4;
см4;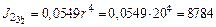 см4;
см4;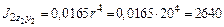 см4.
см4. и
и 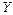 :
: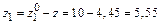 см;
см;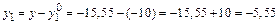 см;
см;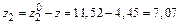 см;
см;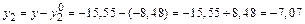 см.
см.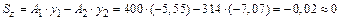 ;
;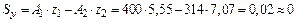 .
.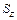 и
и 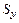 равны нулю. Это свидетельствует о том, что координаты центра тяжести заданной фигуры определены правильно.
равны нулю. Это свидетельствует о том, что координаты центра тяжести заданной фигуры определены правильно.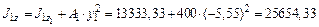 см4;
см4;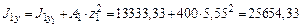 см4;
см4;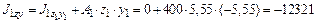 см4;
см4;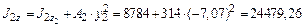 см4;
см4;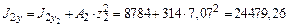 см4;
см4;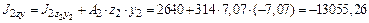 см4;
см4;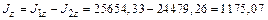 см4;
см4;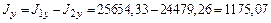 см4;
см4;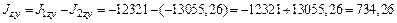 см4.
см4.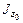 ,
, 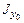 и
и 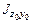 для всей фигуры относительно вспомогательных координатных осей
для всей фигуры относительно вспомогательных координатных осей 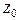 ,
,  , используя при этом формулы перехода к параллельным осям:
, используя при этом формулы перехода к параллельным осям: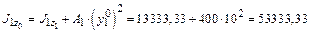 см4;
см4;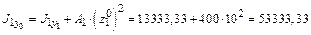 см4;
см4;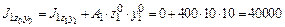 см4;
см4;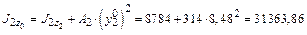 см4;
см4;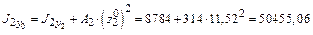 см4;
см4;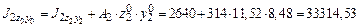 см4;
см4;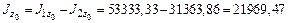 см4;
см4;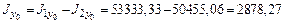 см4;
см4;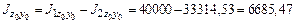 см4.
см4.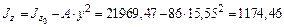 см4;
см4;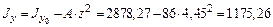 см4;
см4;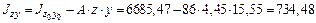 см4.
см4.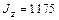 см4;
см4;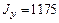 см4;
см4;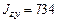 см4.
см4.


