Определение положения центра тяжести фигуры.
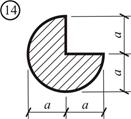
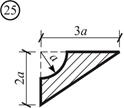
Заданное несимметричное сечение необходимо разбить на отдельные простейшие фигуры, площади и положения центров тяжести которых известны (см. Приложение). В нашем случае таких отдельных элементов будет два: 1) квадрат со стороной 2) четверть круга радиусом
Рис. 2
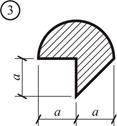
Рис. 3
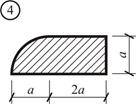
Рис. 4 Выберем произвольно вспомогательную прямоугольную систему координат
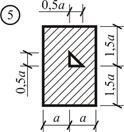
Рис. 5 Определим геометрические характеристики отдельных элементов фигуры (см. Приложение): · площадь 1) квадрат: 2) четверть круга: 3) общая площадь фигуры: · координаты центров тяжести в осях 1) квадрат:
2) четверть круга:
Координаты центра тяжести всего сечения относительно выбранных координатных осей
На чертеже (рис. 5) в выбранном масштабе наносим положение центра тяжести всего сложного сечения (точку С) и указываем величины координат
|

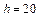 см (рис. 2 а);
см (рис. 2 а);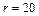 см (рис. 2 б).
см (рис. 2 б).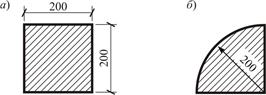

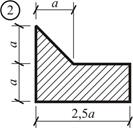
















 . Через центры тяжести каждого элемента (
. Через центры тяжести каждого элемента (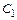 ,
,  ) проводим горизонтальные (
) проводим горизонтальные ( и
и  ) и вертикальные оси координат (
) и вертикальные оси координат ( и
и  ), параллельные осям
), параллельные осям 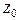 и
и  (см. рис. 5).
(см. рис. 5).
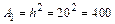 см2;
см2; см2;
см2;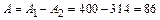 см2;
см2; см;
см; 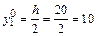 см;
см; см;
см;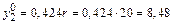 см.
см.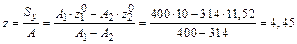 см;
см;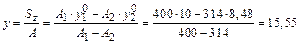 см.
см.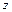 и
и 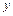 . Через точку С проводим центральные оси
. Через точку С проводим центральные оси  и
и 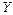 , параллельные вспомогательным осям
, параллельные вспомогательным осям 


