Определение положения главных центральных осей и главных центральных моментов инерции фигуры.
Определим величины главных центральных моментов инерции всего сечения
Произведем проверку полученных вычислений по формуле
Следовательно, сходимость вычислений точная, однако это еще не дает основания считать, что величины главных центральных моментов инерции определены верно. Найдем значения углов, которые образуют главные оси · угол, образованный главной осью
· угол, образованный главной осью
Проверим правильность найденных углов по формуле
При этом возможны два варианта нахождения угла 1) осевые моменты инерции относительно центральных осей равны между собой, т. е.
2) осевые моменты инерции относительно центральных осей не равны между собой, т. е.
В обоих случаях будем иметь два значения угла В нашем случае, вследствие равенства осевых моментов инерции относительно центральных осей будем иметь
что полностью соответствует найденным выше значениям углов, следовательно, направление главных осей На чертеже (рис. 6) в выбранном масштабе через точку С проводим главные центральные оси, поворачивая центральную горизонтальную ось
Рис. 6 В качестве проверки определим величину центробежного момента инерции всего заданного сечения относительно центральных осей
Полученное значение центробежного момента инерции совпадает с ранее найденной величиной. Проверим равенство нулю центробежного момента инерции всего заданного сечения относительно главных центральных осей
Две последние проверки позволяют считать, что величины главных центральных моментов инерции ПРИЛОЖЕНИЕ Таблица П1. Геометрические характеристики плоских сечений
Продолжение табл.П1
|

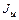 и
и  по формулам:
по формулам: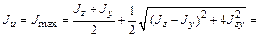
 см4;
см4;
 см4;
см4;
 см4;
см4;  см4.
см4. и
и  с центральной горизонтальной осью
с центральной горизонтальной осью  , т. е., другими словами, определим направление главных центральных осей
, т. е., другими словами, определим направление главных центральных осей 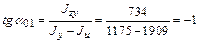 ;
; ;
; ;
;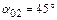 .
. .
. , на который необходимо повернуть центральные оси
, на который необходимо повернуть центральные оси 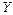 , чтобы определить положение главных центральных осей
, чтобы определить положение главных центральных осей  . Тогда
. Тогда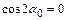 ;
; . Тогда
. Тогда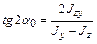 .
.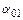 ,
,  ), отличающиеся на 90°, причем меньший из этих углов по абсолютной величине не превышает 45°.
), отличающиеся на 90°, причем меньший из этих углов по абсолютной величине не превышает 45°.
 ,
,
 см4.
см4. .
.

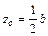



 *
*








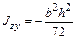 **
**





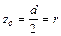


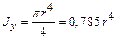




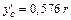



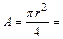
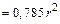


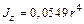

 **
**



