Геометрические модели произвольных границ достаточно сложные, поэтому обычно предлагаются к рассмотрению более простые, особые модели границ.
Если в простой кубической решетке два зерна по разные стороны от грани куба повернуть вокруг вектора ω;, лежащего в плоскости грани {100}, симметрично, т.е. на один угол, то получится граница, называемая симметричной границей наклона. Она относится к простейшим границам, имеющим одну степень свободы, характеризующуюся углом поворота одной решетки относительно другой. Согласно такой схеме (рис. 3.3) в кристалле симметрично относительно грани куба (010) вырезан клин с углом θ;. Поворот каждой части кристалла вокруг вектора ω;, совпадающего на рис. 3.3 с осью Х, на угол θ/2 приводит к образованию симметричной наклонной границы с одной степенью свободы.
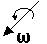
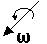
Рис. 3.3. Схема образования симметричной границы наклона;
вектор поворота ω; лежит в плоскости границы
3.2.1. Малоугловые границы наклона
Наиболее просто наклонную малоугловую симметричную границу с одной степенью свободы можно представить в виде стенки краевых дислокаций. Атомное строение такой границы можно проиллюстрировать следующим образом. Срежем часть кристалла с кубической решеткой по плоскости, расположенной под углом θ/2 к поверхности параллельно направлению {100}. На наклонной поверхности кристалла появятся периодические ступеньки (рис. 3.4) с расстоянием
 . .
| (3.1)
|
Тогда число ступенек на единицу длины ρ =1/АВ (плотность ступенек) зависит от угла среза θ/2 и равно
 . .
| (3.2)
|
Рис. 3.4. Ступенька на поверхности, расположенной под углом θ/2 к грани {100} кристалла с ГЦК решеткой

Когда два кристалла с такими ступенчатыми поверхностями (рис. 3.5, а) состыкуются, произойдет упругое сопряжение их решеток (рис. 3.5, б) с небольшим искажением за исключением края ступенек, которые превратятся в экстраплоскости, оканчивающиеся краевыми дислокациями с вектором Бюргерса, равным высоте ступеньки (рис. 3.4).
а б в
Рис. 3.5. Строение малоугловой симметричной границы наклона;
а - два кристалла, разориентированные на угол θ;,
б - граница - дислокационная стенка с экстраплоскостями А, В, С (010),
в – граница ВЕ в модели жестких шаров
Область разделения двух кристаллов – граница является стенкой дислокаций одного знака. Кристаллы симметрично развернуты относительно границы на малые углы + θ/2 и - θ/2 вокруг вектора поворота ω;, совпадающего с направлением [100], с суммарным углом θ;. Положение границы относительно одного из зерен характеризуется одним углом или одной степенью свободы.
Подставляя h = b в формулу (3.2), получаем число дислокаций в обоих зернах на единицу длины границы или плотность дислокаций:

| (3.3)
|
Если угол разориентировки мал, то плотность дислокаций
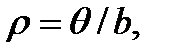 (3.4)
(3.4)
а средне расстояние между дислокациями
 (3.5)
(3.5)
Эта граница представляет собой «полигонизационную стенку» из дислокаций типа описанной в разд. 2.9. Такие границы с малым углом разориентировки, образованные стенкой дислокаций, называются малоугловыми границами, существование которых подтверждается экспериментально.
3.2.2. Энергия малоугловой границы
Шокли и Рид вычислили энергию такой конфигурации, считая, что она находится в бесконечной среде с модулем сдвига μ; и коэффициентом Пуассона v. По их расчетам энергия такой границы на единицу площади равна
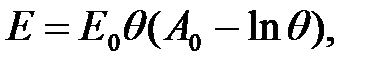
| (3.6)
|
где

| (3.7)
|
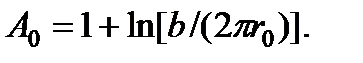
| (3.8)
|
Длина r0 в соотношении (3.8) связана с энергией ядра отдельной дислокации в границе. Согласно уравнению (3.4), для малых θ; плотность дислокаций в границе равна θ/b поэтому первый член в уравнении (3.6) зависит от суммарной энергии ядер дислокаций, отнесенной к единице площади границы. Во второй член входит упругая энергия границы. Напряжения, обусловленные дислокациями, в значительной мере компенсируют друг друга на расстояниях от границы, превышающих расстояние θ/b между отдельными дислокациями в границе. Упругая энергия внутри цилиндра радиусом b/θ;, окружающего краевую дислокацию с радиусом ядра rг, равна
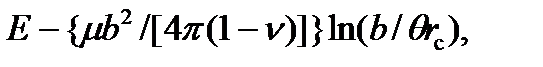
| (3.9)
|
чем и определяется второй член в формуле (3.6).
Формулой (3.6) можно пользоваться только для границ с малым углом наклона θ;, в которых ядра дислокаций не перекрываются.
3.2.3. Малоугловая граница с двумя степенями свободы
Малоугловая граница с двумя степенями свободы получается следующим путем (рис. 3.6).
Рис.3.6. Схема получения границы с двумя степенями свободы (б) из симметричной малоугловой границы с одной степенью свободы (а)
Имеем два зерна P и Q, разделенные симметричной границей ВЕ, заданной нормалью ВN, с углом разориентировки плоскостей (010), равным θ; (см.рис. 3.6). Не изменяя относительной ориентировки зерен с углом поворота θ; одного зерна относительно другого (одна степень свободы), поворачиваем границу ВЕ на рис. 3.6(б) вокруг оси поворота ω; [100] на угол (90 – φ;). Угол поворота, задающий новое положение границы относительно решетки, определяет вторую степень свободы.
Угол φ; - угол между нормалью ВN, задающей ориентировку исходной, симметричной границы (среднее между направлениями [010] двух зерен), и плоскостью границы в новом положении. Эта граница образует угол φ + θ; /2 с направлением [010] в Q зерне и φ - θ; /2 с направлением [010] в зерне P. Поворот границы на угол (90 – φ;) приводит к появлению второй системы дислокаций, экстраплоскости которых перпендикулярны экстраплоскостям первой системы, образовывавшей симметричную границу.
Действительно, плоскости (010), расположенные перпендикулярно катетам АВ и ВС, оканчивающиеся на границе ВЕ, являются экстраплоскостями для дислокаций первой системы, образующих симметричную малоугловую границу ВЕ (рис. 3.6, а). Их количество равно
(АВ + ВС)/ d,
где d межплоскостное расстояние, в примитивной кубической решетке равное вектору Бюргерса b1 первой системы.
После поворота границы плотность дислокаций первой системы ρ1 изменится, и будет определяться разностью длин катетов ВС и EF, т.к. экстраплоскости, проходящие через ВС и ЕF к границе ВЕ, будут с небольшой упругой деформацией восстанавливаться до целых плоскостей (рис. 3.7), а избыток со стороны большего катета ВС составит первую систему дислокаций.
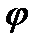

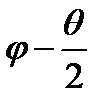
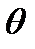
Рис. 3.7. Несимметричная наклонная граница
Из рисунка 3.7. видно, что
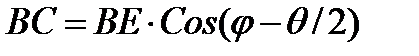 , ,
| (3.10)
|
 . .
| (3.11)
|
Если принять ВЕ =1, то число вертикальных плоскостей, оканчивающихся на единице длины границы ВЕ, т.е. плотность дислокаций
где b1 - вектор Бюргерса первой системы дислокаций.
Аналогично определяется плотность дислокаций второй системы ρ2, которую образуют горизонтальные плоскости (001), оканчивающихся на единице длины границы зерна ВЕ, определяется разностью катетов ЕС и ВF.
где b2 - вектор Бюргерса второй системы дислокаций (в кубической решетке b1 = b2).
Таким образом, при нарушении симметричного расположения решетки по обе стороны границы в результате поворота ее нормали на угол φ; возникает две системы краевых дислокаций, причем, экстраплоскости новой системы (001) нормальны к экстраплоскостям (010) исходного первой системы.
3.2.4. Высокоугловые границы наклона
С увеличением угла разориентировки плотность дислокаций растет, при θ; > 10° расстояние между дислокациями становится равным нескольким межплоскостным расстояниям, при котором их ядра начинают перекрываться, и теряется смысл говорить об отдельных дислокациях. Поэтому дислокационная модель неприменима для описания строения границы зерен с большим углом разориентировки.
С появлением разориентировки между двумя участками решетки, т.е. с образованием границы, происходит изменение энергия решетки. По мере роста угла разориентировки от нулевого значения θ;=0 энергия границы первоначально круто растет, достигает максимума и затем стремиться к некоторому минимальному значению (рис. 3.8.).
Физический смысл интенсивного роста энергии границы наклона заключается в том, что при больших расстояниях между дислокациями поля напряжений каждой отдельной дислокации простираются на довольно значительные расстояния. При росте угла в пределах малых значений количество дислокаций растет, и суммарная энергия границы растет, но их поля не перекрываются. По мере дальнейшего роста угла разориентировки, возрастание энергии замедляется, потому что при сближении дислокаций их поля напряжений накладываются друг на друга и компенсируются.
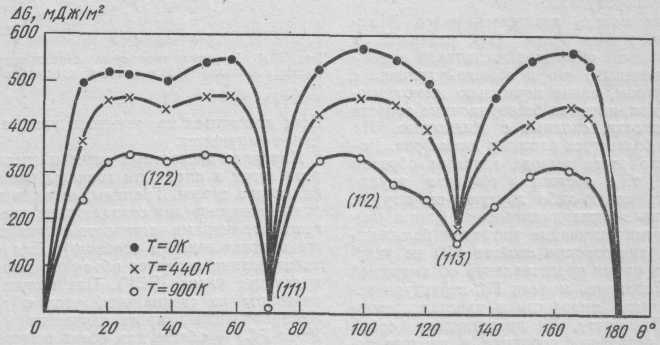
Рис. 3.8. Зависимость свободной энергии границ наклона <110>
в алюминии (машинное моделирование)
При характерных для каждой решетки углах наклона возникает равномерное распределение дислокаций, и на зависимости энергии границы зерна от угла разориентировки должны появляться минимумы. Такое изменение энергии границ кристаллографически разориентированных зерен соответствует представлениям о специальных (особых) границах, отвечающих некоторым особым разориентировкам соседних зерен и обладающих пониженной энергией благодаря более совершенному строению, чем произвольные границы (границы общего типа).
3.2.5. Специальные большеугловые границы наклона, РСУ
Специальную границу можно получить следующим образом. Возьмем два кристалла (зерна) с кубическими решетками и срежем их по плоскостям параллельно направлению [100]. Получится ступенчатая поверхность с длиной ступенек, имеющих одинаковое количество атомов в ступеньке, зависящее от величины угла среза. Расположение атомов на вершинах ступенек характеризуется строгой периодичностью. Для получения границы соединим кристаллы так, чтобы узлы на углах ступенек совпали. Для узлов совпадения, периодически расположенных на границе, в обоих соседних кристаллах в разные стороны от границы найдутся идентичные узлы, которые можно объединить в собственную трехмерную решетку, не изменяющуюся при переходе через границу между кристаллами - когерентную решетку. Такая когерентная решетка или сверхрешетка еще называется решеткой совпадающих узлов (РСУ) или решеткой совпадения. Таким образом, специальные границы должны характеризоваться высокой симметрией при определенном угле разориентировки θ;.
Если число атомов в «ступеньке» превышает 10, как показано рис. 3.4, то границу целесообразно представлять в виде стенки краевых дислокаций. Когда длина ступеньки составляет 6 атомов или меньше, для описания границы следует привлекать понятие РСУ. Ступенькам с малым целым числом атомов (6, 5, 4 и т. д.) соответствует небольшой размер элементарной ячейки решетки совпадения, т.к. при уменьшении длины ступеньки расстояние между узлами на вершинах, являющееся параметром РСУ, уменьшается. Соответственно углы разориентации θ; кристаллов растут достаточно быстро.

Рис. 3.9. Получение РСУ: а – два кристалла со ступенчатыми поверхностями (вершины ступенек обозначены чёрными кружками); б – граница (чёрные кружки с ободками) после соединения кристаллов и РСУ (решётка из чёрных кружков).
В качестве характеристики РСУ («сверхрешетки») используют понятие «степень несовпадения» Σ - число несовпадающих узлов в основной решетке, приходящихся на один узел совпадения. На рис. 3.9 элементарная ячейка когерентной решетки содержит 5 узлов (Σ=5), 4 – внутри ячейки (белые) и один вершинный - совпадающий (черный). Величины Σ и θ; зависят от типа кристаллической решетки и различны для разных осей поворота. В табл. 3.1 приведены значения Σ и θ; для некоторых наиболее часто встречающихся в кубических решетках РСУ.
Часто также используют другое понятие - плотность совпадающих узлов, являющееся обратной величиной Σ. Характерным дискретным углам поворота соответствует определенная плотность совпадающих узлов, т. е. их доля по отношению ко всем узлам решетки металла. Например, на рис. 3.9 при угле поворота 36,9° (37°) вокруг оси <001> РСУ образована каждым пятым атомом соседних зерен, т. е. плотность совпадающих узлов равна 1/5.
Обычно рассматривают решетки совпадающих узлов при значениях Σ, находящихся в интервале 3-25 (при Σ = 1 угол разориентировки равен нулю). Для примера на рис. 3.10 изображена 28-градусная граница в г.ц.к – кристалле с осью наклона [100] и плоскостью (100), лежащей в плоскости рисунка.
| Таблица 3.1
|
| Специальные углы θ; и степень несовпадения Σ для некоторых осей разворота в ОЦК и ГЦК решетках
|
| Ось разворота
| θ
| Σ
| Ось разворота
| θ
| Σ
|
| <100>
| 36,9
22,6
28,1
|
| <111>
| 86,6
26,5
60,0
38,2
27,8
46,8
|
|
| <110>
| 70,5
38,9
50,5
|
|
Рис. 3.10. Специальная наклонная граница с углом 28° в плоскости
исходных зерен (035); АВ - узлы совпадения, РСУ с Σ=17
Ступенька в такой границе лежит в плоскости  и имеет длину в четыре межатомных расстояния в этой плоскости, а высота - одно межатомное расстояние. Угол наклона θ;/2 плоскости
и имеет длину в четыре межатомных расстояния в этой плоскости, а высота - одно межатомное расстояние. Угол наклона θ;/2 плоскости 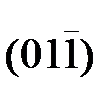 (пунктирная) к границе составляет 14°, а плоскости (001) 59°. Плоскость границы располагается в плоскости (035) исходной решетки симметрично относительно решеток обоих кристаллов и характеризуется периодичностью узлов в плоскости (035) с периодом АВ, соответствующим расстоянию между угловыми узлами ступеньки. Эти узлы образуют РСУ, имеющую Σ=17 (16 внутри – помечены 1…16 и один вершинный - черный).
(пунктирная) к границе составляет 14°, а плоскости (001) 59°. Плоскость границы располагается в плоскости (035) исходной решетки симметрично относительно решеток обоих кристаллов и характеризуется периодичностью узлов в плоскости (035) с периодом АВ, соответствующим расстоянию между угловыми узлами ступеньки. Эти узлы образуют РСУ, имеющую Σ=17 (16 внутри – помечены 1…16 и один вершинный - черный).
Однако в модели жестких шаров (рис 3.11) такая граница должна иметь повышенную энергию из-за наложения шаров f и r (выделено серым) рядом с совпадающими узлами А и В и пустот в местах несопряжений. Гейтлером и Чалмерсом была предложена модель, уменьшающая энергию такой границы. Схематично такую минимизацию на 37° границе в плоскости (012) в ГЦК решетке (рис. 3.11, а) можно проиллюстрировать следующим образом.
б
Рис. 3.11. Схема уменьшения энергии 37° градусной наклонной границы,
а – исходная граница с повышенной энергией,
б – сдвиг зерен по границе (жесткая релаксация).
На первой стадии минимизации в плоскости границы происходит смещение одного зерна относительно другого в положение, изображенное на рис.3.11(б), при котором атомы, находящиеся в вершинах ступеньки одного кристалла, смещаются в углы ступеньки другого, что приводит к устранению наложения атомов f и r и улучшает контакт между атомами на границе. Эта стадия названа «жесткой релаксацией», поскольку каждый атом по-прежнему занимает свой узел в решетке своего собственного зерна. На второй стадии (на рис. 3.11 не показано) под действием сил взаимодействия протекает «атомная релаксация». Атомы, образующие границу под действием атомных сил притяжения и отталкивания смещаются на малые расстояния, и устанавливается их равновесное положение с минимальной энергией.
3.3. Зернограничные дислокации
При отклонениях от симметричной ориентации зерен относительно границы или при стыковке ступенчатых поверхностей с небольшим отличием количества атомов в ступеньке на специальной границе появляется несопряженность. На рис. 3.12 изображена граница в ГЦК решетке с длиной ступенек в три и в четыре атома. Вектор поворота границы ω; совпадает с направлением [100] и перпендикулярен плоскости рисунка, плоскость границы параллельна плоскости зерен (021), ступеньки лежат в плоскости (011). Несопряженность на границе должна приводить к значительной деформации решетки. Для восстановления хорошего сопряжения зерен необходимо компенсировать эту несопряженность вводом экстраплоскости (021), оканчивающейся на границе сидячей дислокацией, т.к. ее вектор Бюргерса не лежит в плоскости скольжения. Из рис. 3.12. видно, что увеличение длины ступеньки соответствует появлению лишней атомной плоскости, обрывающейся на ступеньке, т.е. эксраплосксти. Такая дислокация называется зернограничной дислокацией.

Рис. 3.12. Зернограничные дислокации на границе с различной длиной ступенек в ГЦК решетке
3.4. Сегменты повторяемости
Дальнейшим развитием модели узлов совпадения, в которой делается разграничение между особыми («специальными») границами и случайными («произвольными»), является модель границ зерен, состоящих из структурных единиц или «сегментов повторяемости» (рис.3.13). Поскольку все ступеньки в наклонных симметричных границах равны по длине, это означает, что граница имеет периодическое строение, причем период повторяемости вдоль границы равен расстоянию между краями ступенек. В глубину период повторяемости равен расстоянию между повторяющимися плоскостями кристаллов (например, 2 для плоскостей {100} и {110} и 3 для плоскостей {111} в гранецентрированной кубической структуре). Конфигурация двух соединенных ступенек является «единицей повторяемости» двумерной периодической структуры. Следовательно, границу можно рассматривать как состоящую из идентичных «сегментов», каждый из которых представляет собой единичную полоску двумерной периодической структуры. При отклонении от идеальной ориентировки граница состоит из смеси различной длины сегментов повторяемости в определенной пропорции. Это объясняет факт постепенного, а не скачкообразного изменения свойств границ по мере отклонений ориентировки от особой.

 а
а  б
б
Рис. 3.13. Сегменты повторяемости (структурные единицы):
а -для ориентировок 28,1 и 36,9 град; б - построенная из сегментов повторяемости различных типов структура участка границы с углом разориентировки, не отвечающим идеальным условиям узлов совпадения
Размер единичного сегмента зависит не только от размера элементарной «свехъячейки», но также от наклона границы, т. е. от ориентации ее относительно сверхрешетки. С помощью сегментов повторяемости можно сконструировать границу, которая располагается несимметрично относительно решеток соприкасающихся кристаллов. Такая граница может состоять из сегментов разных типов и различной протяженности сверхрешетки совпадения. Например, несимметричная граница на рис. 3.14 образована общей сверхрешеткой с одними сегментами на участках AB и CD и другими на участке BC. Отдельные участки – “фасетки“, состоящие из одного или нескольких сегментов повторяемости определяют “фасеточную“ структуру асимметричной границы.
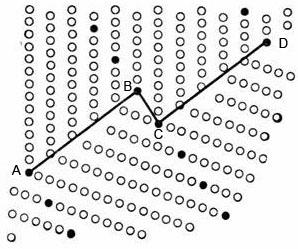
Рис. 3.14. Фасеточные границы, составленные из сегментов
повторяемости различного типа с общей сверхрешеткой
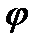

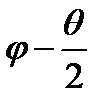
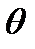

 .
.
 .
.

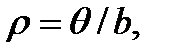 (3.4)
(3.4) (3.5)
(3.5)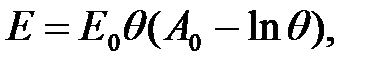

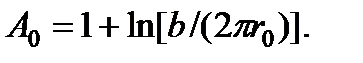
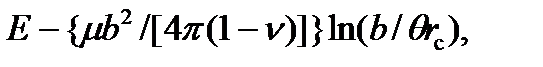
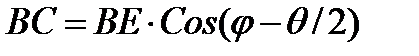 ,
,
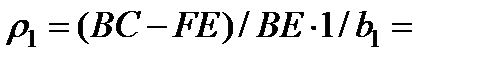
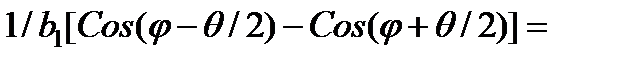




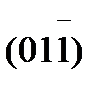
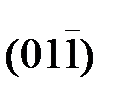 и имеет длину в четыре межатомных расстояния в этой плоскости, а высота - одно межатомное расстояние. Угол наклона θ;/2 плоскости
и имеет длину в четыре межатомных расстояния в этой плоскости, а высота - одно межатомное расстояние. Угол наклона θ;/2 плоскости 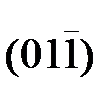 (пунктирная) к границе составляет 14°, а плоскости (001) 59°. Плоскость границы располагается в плоскости (035) исходной решетки симметрично относительно решеток обоих кристаллов и характеризуется периодичностью узлов в плоскости (035) с периодом АВ, соответствующим расстоянию между угловыми узлами ступеньки. Эти узлы образуют РСУ, имеющую Σ=17 (16 внутри – помечены 1…16 и один вершинный - черный).
(пунктирная) к границе составляет 14°, а плоскости (001) 59°. Плоскость границы располагается в плоскости (035) исходной решетки симметрично относительно решеток обоих кристаллов и характеризуется периодичностью узлов в плоскости (035) с периодом АВ, соответствующим расстоянию между угловыми узлами ступеньки. Эти узлы образуют РСУ, имеющую Σ=17 (16 внутри – помечены 1…16 и один вершинный - черный).
 а
а  б
б



