Силы, действующие на дислокацию 1 страница
В результате приложения к кристаллу внешних напряжений появляется сила F, действующая на дислокацию внутри кристалла вдоль плоскости скольжения перпендикулярно линии дислокации, какой бы сложной по форме она ни была. При этом она ориентирована в кристалле в том направлении, куда дислокация еще не пришла, и находится следующим образом. Рассмотрим линейную дислокацию. Если к кристаллу, содержащему дислокации, приложить достаточное напряжение, дислокации начнут двигаться, и произойдет пластическая деформация. В процессе движения дислокаций приложенное напряжение выполняет работу. Под действием однородного касательного напряжения t от внешней силы верхняя часть кристалла сдвигается относительно нижней части на величину b по площади S=L×x, где
Этот сдвиг происходит в результате движения дислокации длиной L по всей ширине на пути х под действием силы F. Поэтому сила, действующая на дислокацию и приводящая ее в движение:
а на единицу длины дислокации действует сила
Под действием приложенного внешнего напряжения дислокация может выгибаться в дугу (рис. 2.23). Любое увеличение длины дислокации приводит к повышению энергии, поэтому существует линейное натяжение дислокации, стремящееся выпрямить эту дугу. Пусть элемент дислокации под действием напряжения t, направленного от О к В, изогнулся в дугу dl. Сила натяжения Т будет стремиться выпрямить эту дугу.
Условия равновесия
Так как
или
Полученное соотношение, связывающее величину радиуса дуги изогнутой дислокации с величиной касательного напряжения от действия внешних сил, очень важно для изучения процессов упрочнения металлов. 2.9. Взаимодействие дислокаций Вокруг дислокаций решетка упруго искажена и поле напряжений одной дислокации действует на соседнюю дислокацию, находящуюся в параллельной плоскости скольжения с силой f=bt. Рассмотрим две параллельные краевые дислокации А и В с параллельными векторами Бюргерса, лежащие в параллельных плоскостях скольжения Р1 и Р2 (рис. 2.24). Их взаимодействие определяется величиной силы f с компонентами fх – в направлении скольжения и fу – перпендикулярно плоскости скольжения
Рис. 2.24. Силы взаимодействия между двумя краевыми дислокациями
Так как краевая дислокация может перемещаться скольжением только в плоскости, содержащей линию дислокации, то для определения взаимодействия дислокаций наиболее важна компонента силы fх
где txy = tyx напряжение из (2.19) первой дислокации с b2 - вектор Бюргерса второй дислокации. Пусть взаимодействующие дислокации находятся в параллельных плоскостях, удаленных друг от друга на расстояние h (рис. 2.25). Учитывая, что дислокации параллельны и b1 = b2, то сила, с которой первая дислокация, условно закрепленная в начале координат, действует на вторую подвижную дислокацию, равна
Знак в формуле (2.38) определяется знаком векторов Бюргерса дислокаций. Если обе дислокации имеют один знак, то произведение их векторов будет положительным, если разные знаки — отрицательным. Придавая координате x различные значения x = h; 0 < x < h; x = 0; ‑h < x < 0; x = -y, построим кривую изменения силы fх действия первой дислокации на вторую в зависимости от расстояния x между ними: fx = f(x). Имеем дислокации одного знака. Вторая дислокация находится в параллельной плоскости скольжения В, справа от первой дислокации, закрепленной в начале координат, х ≥ 0. Если х = 0 и х = h, то согласно (2.38) fx =0, и между дислокациями взаимодействие отсутствует. В интервале 0 < x < h числитель дроби отрицательный, следовательно, сила fx отрицательна и направлена в противоположную сторону относительно направления х, поэтому под ее действием вторая дислокация будет двигаться в направлении первой, т.е. притягиваться. Учитывая, что на краях интервала 0 < x < h сила fх = 0, тогда изменение силы взаимодействия на этом интервале можно изобразить кривой с минимумом. При х > h сила действия первой дислокации на вторую совпадает с направлением х, и под ее влиянием вторая дислокация будет удаляться от первой, т.е. дислокации отталкиваются. При больших значениях х взаимодействие исчезает и fx стремиться к 0, следовательно, правее х = h кривая fx изображается с максимумом.
Рис. 2.25. Сила, действующая между параллельными одного (а) и разных (б) знаков краевыми дислокациями в параллельных плоскостях скольжения, отстоящих друг от друга на расстоянии h Если вторая дислокация расположена левее первой х ≤ 0, направление действия силы меняется на противоположное, как это изображено на рис. 2.25, а. Из графика видно, что в интервале ‑h < x < h вторая дислокация притягивается к первой, и при х = 0 существует устойчивое равновесие. При х = h существует неустойчивое равновесие. Если дислокации имеют противоположные знаки, то интервалы действия сил притяжения и отталкивания изменяются и силы притяжения и при х = 0 возникает неустойчивое равновесие, а при х = h –устойчивое (рис. 2.25, б). Следовательно, устойчивое положение дислокаций достигается в том случае, если краевые дислокации одного знака располагаются друг над другом (x =0), образуя дислокационную стенку. Такая стенка представляет собой малоугловую границу наклона, которая делит кристалл на два фрагмента. Угол разориентировки (наклона) этих фрагментов равен
где При нагреве деформированных металлов и сплавов и достаточном избытке дислокаций одного знака наблюдается процесс образования малоугловых границ, получивший название полигонизация. Для краевых дислокаций противоположных знаков выражение (2.38) отрицательно, и дислокации взаимно притягиваются вдоль плоскостей скольжения при х > h, отталкиваются при х < h (рис. 2.25, б). Поэтому равновесие устойчиво при х = h и неустойчиво при х = 0, т.е. для дислокаций разных знаков устойчивым будет такое положение, при котором радиус-вектор, соединяющий ядра дислокаций, образует с плоскостью скольжения угол J = 45°. Такая устойчивая конфигурация, которую дислокации стремятся приобрести в кристалле, показана на рис. 2.26.
Отсюда видно, что дислокации одного знака будут взаимно отталкиваться с силой, обратно пропорциональной расстоянию между ними, и располагаться вдали друг от друга (рис. 2.27, а), а разных знаков - притягиваться и аннигилировать (рис. 2.27, б, в). Для дислокаций противоположных знаков, расположенных в соседних параллельных плоскостях, энергетически выгодно рекомбинировать (аннигилировать) с образованием целой цепочки точечных дефектов (рис. 2.27, г).
В отличие от краевой дислокации вокруг винтовой имеются только касательные напряжения. Поле этих напряжений симметрично относительно линии дислокации и на расстоянии r от линии дислокации
Сила взаимодействия
Аналогично краевым дислокациям, разноименные винтовые, расположенные параллельно относительно друг друга, взаимно притягиваются и при встрече аннигилируют. Одноименные дислокации стремятся оттолкнуться и удаляются друг от друга, перемещаясь скольжением. Краевая и винтовая дислокации с параллельными векторами Бюргерса взаимно перпендикулярны и между собой не взаимодействуют, так как составляющие касательного напряжения краевой дислокации в направлении вектора Бюргерса винтовой дислокации равны нулю. 2.10. Пересечение дислокаций Движущиеся дислокации встречают на своем пути множество других дислокаций, находящихся в непараллельных плоскостях (лес дислокаций). В этих условиях они могут пересекаться, что приводит к изменению характера дислокационной структуры и упрочнению кристалла. Схемы пересечения двух краевых дислокаций с перпендикулярными векторами Бюргерса, т.е. перпендикулярными экстаплоскостями, представлены на рис. 2.28, а,б.
Рис. 2.28. Схема пересечения краевых дислокаций с взаимно перпендикулярными (а, б) и параллельными (в, г) векторами Бюргерса: Дислокация ХУ с вектором Бюргерса b1, ограничивающая экстаплоскость Еху, движется в плоскости скольжения Рху и пересекает дислокацию АВ с вектором Бюргерса b2, лежащую в плоскости РАВ (экстаплоскость дислокации АВ направлена вниз под РАВ и на рисунке не изображена). При движении дислокации ХУ атомные полуплоскости по одну сторону от плоскости скольжения РХУ (на рис. 2.28 справа) смещаются на вектор Бюргерса b1, и часть Р¢В линии дислокации АВ, лежащая в правой половине плоскости РАВ, сместится вместе с этой полуплоскостью в направлении движения (вниз). Поэтому при пересечении одной краевой дислокацией ХУ другой краевой дислокации АВ на второй дислокации образуется порог РР¢; (рис. 2.28, а,б), подобно тому, который возникал при переползании части краевой дислокации в соседнюю параллельную плоскость (см. рис. 2.13). Величина порога на второй дислокации АВ равна вектору Бюргерса b1 первой дислокации XY. Порог PP′; перпендикулярен вектору Бюргерса b2, следовательно, имеет краевую ориентацию, поэтому движение дислокации АРР¢В в плоскости скольжения РАВ практически не затрудняется. В свою очередь дислокация ХУ до пересечения проходила через n плоскостей. После пересечения ее длина увеличилась на величину одной плоскости, являющейся экстраплоскотью дислокации АВ. Увеличение длины дислокации ХУ равно вектору Бюргерса b2 другой дислокации АВ. Можно считать, что на дислокации также образуется порог, только он вытягивается и совпадает с самой дислокацией. В результате образования порога, энергия дислокации увеличивается пропорционально ее удлинению
и возрастет на величину, равную энергии порога, пропорциональную Gb12b2, или при равных векторах Бюргерса Gb3. Если движутся дислокации с параллельными векторами Бюргерса (параллельными экстраплоскостями) в пересекающихся плоскостях скольжения (рис. 2.28, в,г), то пороги образуются на обеих дислокациях. Каждая из дислокаций удлиняется на одну экстраплоскость с образованием ступеньки равной и параллельной вектору Бюргерса другой дислокации. В этом случае порог имеет винтовую ориентацию. Обычно пересечение дислокаций изображают, как показано на рис. 2.28 (г). На рис. 2.28 а,б две части АР и Р¢В дислокации АВ лежат в параллельных плоскостях скольжения, и дислокация не может выпрямиться скольжением. Поэтому такой порог РР¢; обладает высокой устойчивостью. На рис. 28, в, г обе ветви АР - Р¢В дислокации АВ и XQ - Q¢Y дислокации ХУ лежат в одной плоскости скольжения, и порог неустойчив, так как дислокация стремится уменьшить свою энергию и выпрямиться при скольжении. Такой порог называется перегибом. Пересечение движущейся краевой дислокации с винтовой показано на рис. 2.29, а,б. Краевая дислокация АВ движется в плоскости скольжения Р. Вблизи винтовой дислокации ХУ плоскость скольжения приобретает форму винтовой поверхности, и часть дислокации со стороны точки А будет опускаться по винтовой поверхности, а со стороны точки В – подниматься. При пересечении АВ и ХУ дислокация АВ разрезается на две части АР¢; и РВ, которые продолжают скользить в соседних параллельных плоскостях. Обе части соединены порогом РР¢;, имеющим краевую ориентацию с вектором Бюргерса, совпадающим с направлением скольжения, поэтому порог не будет препятствовать скольжению.
Пробег краевой дислокации АВ в поверхности Р вызывает смещение кристалла над поверхностью на расстояние b 1. Поэтому на линии винтовой дислокации ХУ также появится порог, равный по величине и направлению вектору Бюргерса b1 и перпендикулярный вектору Бюргерса b 2, т.е. имеющий краевую ориентацию. Пересечение двух винтовых дислокаций АВ и ХУ изображено на рис. 2.29, в, г. Дислокация АВ движется в винтовой поверхности и при пересечении с дислокацией ХУ разделится на две ветви АМ и М¢В, лежащие на разных уровнях винтовой поверхности, соединенные порогом ММ¢;. Этот порог имеет такой же вектор b 1, как и вся дислокация AB, следовательно, b 1 перпендикулярен порогу ММ¢;, и он имеет краевую ориентацию. Такой же порог с краевой ориентацией появляется на дислокации ХУ. Порог ММ′;, имеющий краевую ориентацию с таким же, как у дислокации АВ, вектором Бюргерса b 1, может двигаться и вдоль дислокации АВ в направлении b 1, и вместе с дислокацией в направлении u перпендикулярно b 1 (рис. 2.30) Вдоль дислокации АВ порог может легко двигаться, так как движение происходит в плоскости скольжения в направлении вектора Бюргерса b 1. В направлении u движения всей дислокации, т.е. перпендикулярно вектору Бюргерса b 1, порог может двигаться только, если за ним остается цепочка вакансий. Если дислокации движется в противоположном направлении, то за порогом должна оставаться цепочка межузельных атомов.
Поэтому порог движется переползанием, и дислокация, двигаясь в направлении u, тащит за собой порог, который тормозит движение, так как скорость диффузии значительно меньше скорости скольжения дислокации. Дислокация выгибается в сторону порога, а за движущимся порогом остается или цепочка вакансий, или цепочка межузельных атомов. На практике винтовая дислокация пересекает лес дислокации и на ней образуется множество порогов (рис. 2.31). Пороги разных знаков аннигилируют, а одного знака равномерно распределяются вдоль дислокационной линии в результате их взаимного отталкивания. Эти пороги играют роль тормоза дислокации, поэтому, если приложить в направлении скольжения достаточное напряжение, то дислокация будет выгибаться между порогами. Радиус кривизны R дислокации между порогами будет определяться соотношением межу скалывающим напряжением и напряжением, необходимым для образования вакансии или дислоцированного атома.
Образование точечных дефектов при протаскивании порога требует затраты энергии, затрудняет движение дислокации и упрочняет металл. 2.11. Дислокации в реальных металлах До сих пор нами рассматривались различные типы дислокаций применительно к структуре кристалла с простой кубической решеткой. В этой решетке атомы располагаются только в вершинах элементарной кубической ячейки. Однако металлам не свойственна простая кубическая решетка, на примере которой рассматривались геометрия дислокации; для них типичны структуры ГЦК, ГПУ, ОЦК. Строение и движение дислокаций в реальных металлах можно рассмотреть, используя ГЦК решетку. Основные закономерности сохраняются и для ОЦК и ГПУ решеток. 2.11.1. Дефекты упаковки в ГЦК кристаллах Плотноупакованные структуры можно образовать укладкой друг на друга плотноупакованных слоев так, как это схематически показано на рис. 2. 32. На плотноупакованный слой А накладывается следующий слой, например в положение В, (или С). Здесь А, В и С обозначают три возможные положения слоев в проекции, нормальной к плотноупакованным слоям. В плотноупакованных структурах не бывает последовательности слоев с одинаковым положением АА, ВВ … Третий слой при наличии второго слоя в положении В можно положить в положение С или А. Последовательность, соответствующая ГЦК кристаллу, получается при укладке … АВСАВС … или … АСВАСВА …; ГПУ кристаллу — … АВАВАВ …; … ВСВСВС …; САСАСА … Нарушения очередности укладки плотноупакованных плоскостей называется дефектом упаковки
В ГЦК кристаллах плотноупакованные плоскости {111} являются плоскостями скольжения и двойникования. Дефект упаковки - двойник соответствует вращению на 180° в плоскости {111} или, что то же самое, зеркальному отражению в плоскости {111}. Так как буквы А, В, С обозначают плоскости {111}, зеркальная симметрия и, следовательно, двойник легко могут быть представлены в условных обозначениях:
где линией обозначена плоскость двойникования, являющаяся центром дефекта упаковки. Другие дефекты в плоскости {111} являются дефектами упаковки, которые классифицируются по Франку как дефекты вычитания или дефекты внедрения. Дефект упаковки вычитания образуется при удалении одного слоя атомов, например, В из нормальной последовательности АВС:
Дефект упаковки внедрения образуется при введении дополнительного слоя атомов, например, В в правильную последовательность АВС:
В дефекте упаковки типа вычитания нормальная последовательность упаковки в кристалле сохраняется с той или другой стороны дефекта вплоть до плоскости дефекта. В дефекте типа внедрения плоскости, вставленные в центр дефекта, неправильно расположены относительно слоев с обеих сторон дефекта. Такие же дефекты упаковки с низкой энергией и такой же конфигурацией могут быть получены другим способом — сдвигом в плоскостях {111}. Предположим, что плоскость А на рис. 2.31 является плоскостью идеального ГЦК кристалла, а следующая плоскость (лежащая над А) — плоскость В. Если плоскость В и все плоскости выше нее сместятся на вектор b =1/6 [211], то плоскость В сдвинется в положение С, а расположенные выше плоскости перейдут соответственно в положение С®А, А®В, В®С и т.д. относительно первоначального положения, фиксированного на плоскости А. Эти сдвиговые смещения изображены стрелками
При этом получается
В результате как бы удаляется плоскость В и возникает дефект упаковки типа вычитания (2.46), а в ГЦК упаковке … АВСАВС … появится слой … САСА …, отвечающий ГПУ чередованию слоев. Если плоскость С, расположенную ниже А, и все нижние плоскости в конфигурации (2.48) сместить на
то получится дефект типа внедрения:
Другие дефекты, вызванные удалением двух плоскостей, что приводит к последовательности 2.11.2. Полные и частичные дислокации в ГЦК структурах На рис. 2.33 приведена ГЦК ячейка, в которой различным цветом и цифрами обозначены атомы, принадлежащие различным плотноупакованным плоскостям (111) – А, В и С.
|

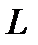 – ширина кристалла, х – протяженность сдвига. Совершаемая при этом работа
– ширина кристалла, х – протяженность сдвига. Совершаемая при этом работа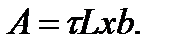
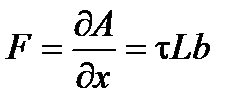 ,
,
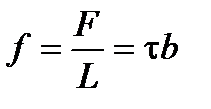
 Рис. 2.23. Схема сил, действующих на дугу дислокации
Рис. 2.23. Схема сил, действующих на дугу дислокации
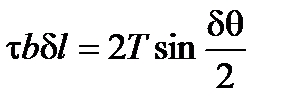 .
.
 , то для малого угла dq, если принимать во внимание уравнение (2.30):
, то для малого угла dq, если принимать во внимание уравнение (2.30):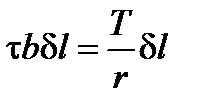
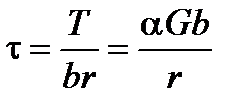 .
.
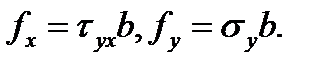
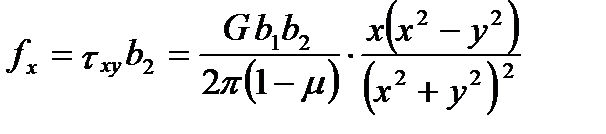 ,
,

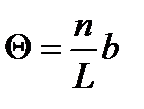 ,
,
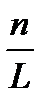 - число дислокаций на единицу высоты дислокационной стенки.
- число дислокаций на единицу высоты дислокационной стенки.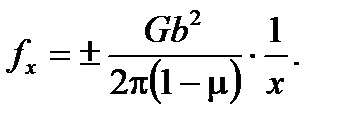
 Рис. 2.26. Устойчивая конфигурация краевых дислокаций разных знаков
Рис. 2.26. Устойчивая конфигурация краевых дислокаций разных знаков

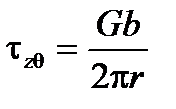 .
.
 .
.

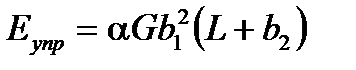


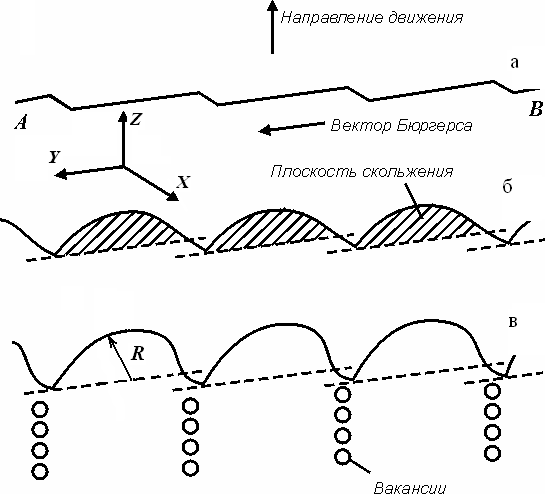
 Рис. 2.32. Порядок укладки плотноупакованных плоскостей в ГЦК решетке: АВСАВС...
Рис. 2.32. Порядок укладки плотноупакованных плоскостей в ГЦК решетке: АВСАВС...
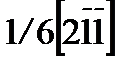 (С®В)
(С®В) , содержат нарушение плотной упаковки в плоскости дефекта, имеют относительно большую поверхностную энергию и маловероятны.
, содержат нарушение плотной упаковки в плоскости дефекта, имеют относительно большую поверхностную энергию и маловероятны.


