Линейные дефекты
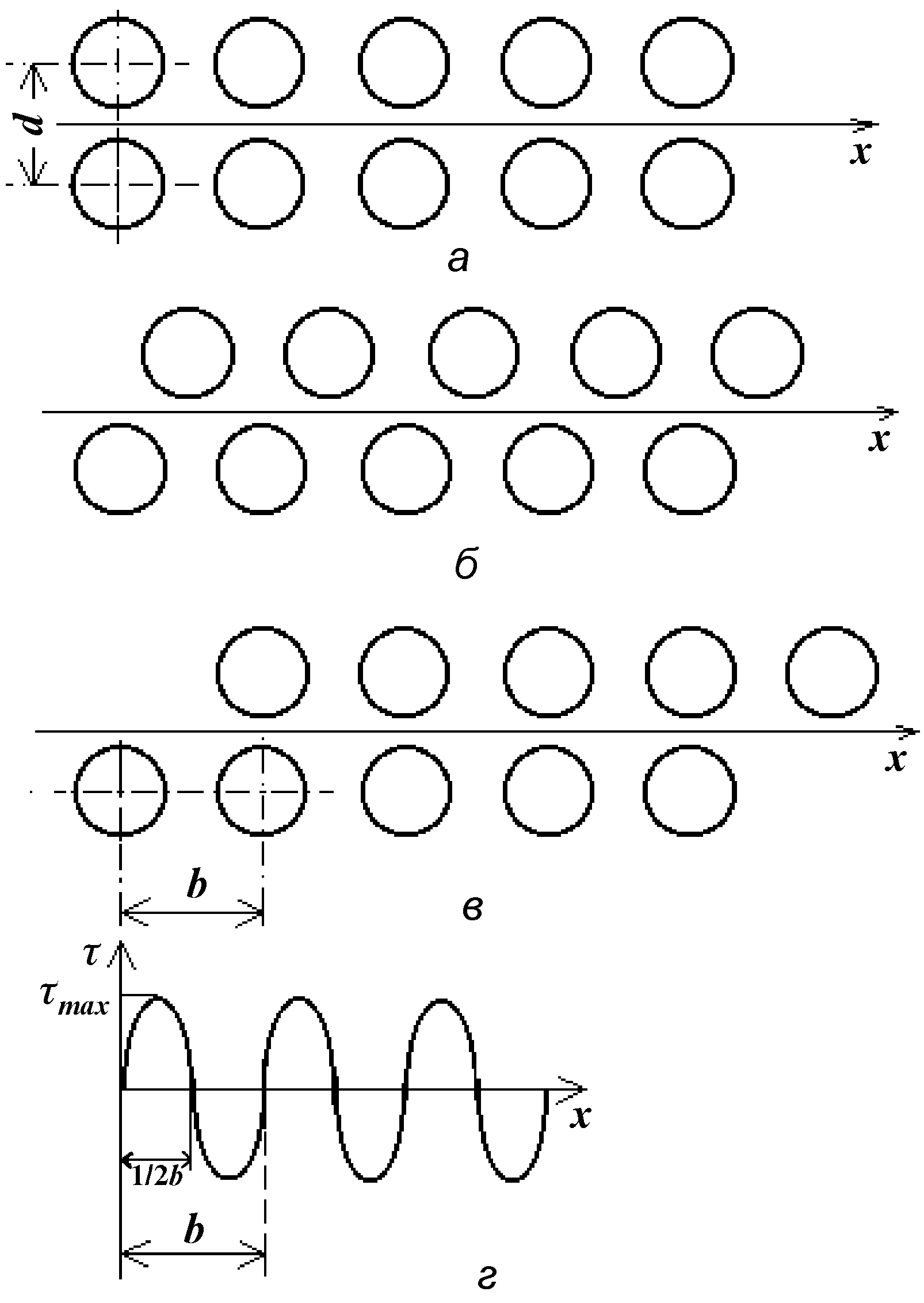
Теория дислокаций играет важную роль при объяснении механических и физических свойств твердых тел. Поэтому решение проблем современной физики металлов невозможно без знаний о природе дислокаций, их свойствах и поведении под действием механической нагрузки и в различных полях. С привлечением теории дислокаций удалось понять механизм пластической деформации металлов и их упрочнение, зарождение и рост кристаллов, а так же объяснить различные процессы в реальных металлах и сплавах при изменении температуры. 2.1. Теоретическая и реальная прочность кристаллов Расчет критического скалывающего напряжения (теоретической прочности) на сдвиг кристалла был проведен Я.И. Френкелем в предположении, что атомы сдвигаются одновременно по всей плоскости скольжения относительно соседней под действием внешнего напряжения, которое работает против сил межатомного взаимодействия. Такой сдвиг называется синхронным или жестким. Полный сдвиг из равновесного положения «а» (рис. 2.1, а) в положение «в» (рис. 2.1, в) происходит через промежуточное положение «б» (рис. 2.1, б). В положении равновесия «а» (рис. 2.1,а) равнодействующая сил атомного взаимодействия равна нулю. В начале сдвига сила межатомного взаимодействия возрастает вследствие того, что атом «e» удаляется от атома «f», достигает максимума, а потом опять снижается до нуля, так как в положении «б» смещенный атом «e» с одинаковой силой притягивается слева и справа соседними атомами «f» и «p» нижней плоскости. Согласно рис. 2.1, б, расположение атомов симметрично, поэтому максимум силы взаимодействия будет находиться посередине между положениями «а» и «б» т.е. при х = b/4. Сила межатомного взаимодействия направлена против сдвигающего напряжения t, так как атом «e» притягивается к атому «f». При дальнейшем смещении из положения равновесия «б» направление силы взаимодействия должно поменять знак, так как атом «e»начинает притягиваться атомом «p» в направлении напряжения t и, проходя через минимум, достигает нуля в новом равновесном положении «с». Поэтому сила сдвига верхней плоскости и соответствующее касательное напряжение находится в синусоидальной зависимости от периода решетки
Постоянный коэффициент k определяется из условия малости смещения x, при котором
По закону Гука для малых сдвигов
где d – межплоскостное расстояние. Приравнивая формулы (2.1) и (2.3), учитывая, что x мало, определяем k и, подставляя его в (2.1), получаем
Рис. 2.1. К расчету критических скалывающих напряжений в идеальном кристалле: а, в – положение атомов до и после сдвига; б – промежуточное равновесное положение атомов; г - синусоидальная зависимость напряжения сдвига от величины смещения (по Френкелю)
Максимальное (критическое) скалывающее напряжение
Межплоскостное расстояние d близко к межатомному расстоянию в направлении сдвига b»d, поэтому
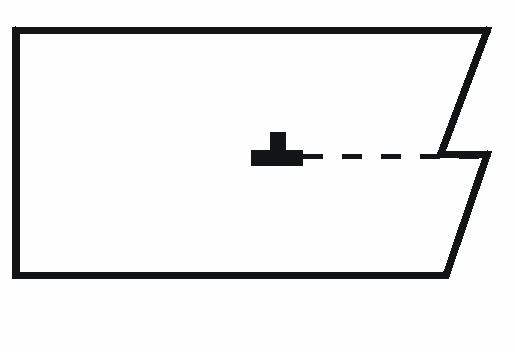
Например, для кристаллов меди G =46,0 кН/мм2, следовательно, теоретическое сдвиговое напряжение по Френкелю составляет 7,6 кН/мм2. В то же время для реальных кристаллов меди сопротивление сдвигу составляет лишь 1,0 Н/мм2. Отсюда видно, что теоретическое значение прочности на несколько порядков выше его действительной величины. Указанное существенное расхождение между рассчитанной и действительной прочностью металлов позволяет считать, что использованная простая модель синхронного сдвига не соответствует поведению реальных кристаллов. 2.1. Полные дислокации Экспериментальные данные свидетельствуют о том, что деформация обычно осуществляется посредством сдвига или скольжения плотноупакованных атомных плоскостей друг относительно друга. Такое скольжение начинается, когда компонента сдвигового напряжения становится больше определенной величины, характерной для данного материала. Из этого следует, что связь между атомами является не жесткой, а упругой. Сдвиг зарождается на отдельных участках плоскости скольжения и затем последовательно распространяется на всю плоскость. Разные части кристалла по одну сторону от плоскости скольжения смещаются на неодинаковые расстояния относительно остального кристалла с другой стороны от плоскости скольжения. Поэтому в работе против внешних сил участвует только небольшая часть атомов. Механизм такого сдвига объясняет теория дислокаций (Орован, Поляни, Тейлор, 1934 г.), при этом на первых этапах развития теории представления о дислокациях были чисто гипотетическими, а прямые доказательства их существования были получены значительно позже. Наиболее простое определение дислокации можно дать следующее: дислокация — это линия в плоскости скольжения, отделяющая с одной стороны от плоскости скольжения часть кристалла, в которой произошло перемещение атомов, от другой части, в которой не произошло перемещения атомов. Рассмотрим строение некоторых видов дислокаций, имеющих большое значение в вопросах прочности и пластичности. 2.1.1. Краевая дислокация Представление о краевой дислокации можно получить из рассмотрения относительно простой модели. На рис. 2.2 показан кристалл, верхняя часть которого сдвинута относительно нижней по плоскости ABCD в направлении Ох1. Скольжение произошло на площади APQD, которая отделена от остальной части плоскости, где скольжение не произошло, линией дислокации PQ. В результате скольжения атомы сместились на расстояние | b | в направлении Ох1. Очевидно, что атомы, примыкающие к линии дислокации PQ выше плоскости скольжения, сжаты, а ниже — растянуты.
Рис. 2.2. Краевая дислокация PQ в кристалле, Атомное строение краевой дислокации для примитивной кубической решетки показано на рис. 2.3. Линия дислокации, отмечаемая значком ^,перпендикулярна атомной плоскости, находящейся в плоскости рисунка. Перемещение, в результате которого часть атомов перешла в соседнее положение и решетка восстановилась, произошло в правой части рисунка. Это перемещение распространяется в плоскости скольжения АВ до области с искаженной кристаллической решеткой, в которой сдвиг затухает, и далее следует недеформированная решетка с совершенным строением. Таким образом, область дефектной решетки, ограничивающая зону сдвига, и есть дислокация.
Рис. 2.3. Краевая дислокация в примитивной кубической решетке в плоскости скольжения AB (внутри окружности находится область со смещенными атомами – дислокация)
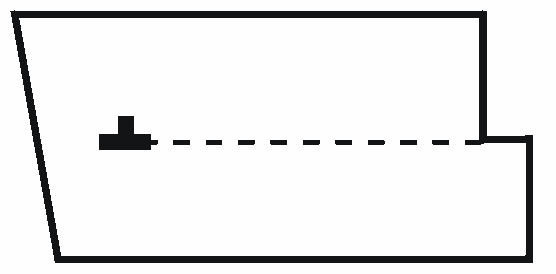
Дислокацию можно представить другим способом. Как видно на рис. 2.3, в верхней части кристалла находится неполная атомная плоскость PF, не имеющая продолжения в нижней половине кристалла. Такую полуплоскость (ее называют экстраплоскостью) можно рассматривать как лишнюю неполную плоскость, вставленную в кристалл. Атом, расположенный на самом краю экстраплоскости, имеет меньше соседей, чем атом внутри совершенной решетки. Поэтому непосредственно вблизи края экстраплоскости решетка сильно искажена; выше края решетка оказывается сжатой, а ниже - растянутой, атомные плоскости, параллельные экстраплоскости, изгибаются, чтобы ниже плоскости скольжения не образовывалась щель. Вдоль края экстраплоскости тянется область, условно обозначенная пунктирной окружностью, где атомы смещены от положения равновесия, создавая линейное структурное несовершенство решетки — краевую дислокацию. Таким образом, обобщая различные определения можно отметить следующее. Дислокация — это граница зоны сдвига в плоскости скольжения. При макроскопическом рассмотрении такая граница зоны сдвига внутри кристалла является геометрической линией (PQ на рис. 2.2), а при микроскопическом рассмотрении — областью несовершенства решетки. Протяженность этого несовершенства в одном направлении такая же, как и длина края экстраплоскости. В плоскости, перпендикулярной краю экстраплоскости, область рассматриваемого несовершенства имеет малые размеры — около 2-10 атомных диаметров. Можно представить, что данная область несовершенства находится внутри своеобразной трубы, осью которой является край экстраплоскости. Вне этой трубы строение кристалла близко к идеальному, а внутри (в так называемом ядре дислокации Лишняя полуплоскость может находиться выше или ниже плоскости скольжения, в первом случае дислокацию условно принято называть положительной краевой дислокацией, во втором — отрицательной. Обе дислокации принято обозначать значками соответственно «^» и «Т». В поле данного напряжения положительная и отрицательная дислокации двигаются в противоположном направлении, создавая сдвиг одного и того же знака. 2.1.2. Винтовая дислокация Вторым основным типом дислокации, который был предложен Бюргерсом в 1939 г., является винтовая дислокация, природу которой можно представить следующим образом. Сделаем в кристалле надрез в плоскости ABCD (рис. 2.4) и произведем сдвиг в части плоскости в верхней половине кристалла в направлении Ох1 на одно межатомное расстояние, при этом верхняя часть кристалла А1PQB1 сдвинется относительно нижней АPQB.
Рис. 2.4. Сдвиг, создающий винтовую дислокацию
Образовавшаяся при таком сдвиге ступенька на боковой грани не проходит через всю ширину кристалла, оканчиваясь в точке Q. Линия РQ, ограничивающая зону сдвига, является винтовой дислокацией. Горизонтальная проекция атомного строения винтовой дислокации в простой кубической решетке показана на рис. 2.5 в соответствии с рис. 2.4. Плоскость рисунка является плоскостью скольжения дислокации PQ. Точки, образованные перекрестиями линий решетки, обозначают атомы под плоскостью, а окружности - атомы над плоскостью скольжения. В идеальной решетке точки и окружности совпадают. Под действием сдвигающего напряжения t часть кристалла A1PQB1 над плоскостью скольжения ADCB сдвигается на одно межатомное расстояние до линии дислокации PQ. На рисунке в линии дислокации атомы над плоскостью скольжения (окружности) на интервале в четыре межатомных расстояния смещаются в направлении t относительно неподвижных атомов (точки перекрестия) под плоскостью скольжения, окружающая дислокацию решетка до и после сдвига остается идеальной.
Рис. 2.5. Атомная структура винтовой дислокации в примитивной кубической решетке
Картина деформации решетки вокруг винтовой дислокации оказывается иной, чем в случае краевой дислокации. Лишней атомной полуплоскости в этом случае нет, а в результате сдвига атомные плоскости в районе дислокации несколько изогнутся, и каждая из них (EB1) над плоскостью скольжения совпадет с ближайшей (B1K) под плоскостью (рис. 2.4). В результате боковая плоскость кристалла окажется как бы образованной единой атомной плоскостью, закрученной по винту enktfr, т.е. из системы дискретных плоскостей они превращаются в непрерывную геликоидальную поверхность. 2.2. Контур и вектор Бюргерса Для однозначного определения дислокации вводится понятие вектор Бюргерса b или вектор смещения дислокации. Вектор Бюргерса b определяется по методу, предложенному Франком. Рассмотрим простую кубическую решетку. Проведем вокруг дефекта, но вдали от него, по узлам неискаженной решетки замкнутый контур afcd произвольной формы — контур Бюргерса (рис. 2.6,а). Перенесем этот контур в идеальный кристалл, не содержащий дефекта строения. Если дефект строения является дислокацией, то контур на участке а'е обязательно окажется незамкнутым. Для того чтобы его замкнуть, надо вставить отрезок, который и называется вектором Бюргерса b (рис. 2.6,б). Дислокацию, следовательно, можно определить не только как границу незавершенного сдвига, но и как такой одномерный дефект, для которого контур Бюргерса в идеальной решетке разомкнут или перезамкнут. Если принять положительное направление линии дислокации идущим вдоль оси, перпендикулярной плоскости рисунка, на нас, то обход контура следует производить против часовой стрелки. Построение контура и вектора Бюргерса для винтовой дислокации показано на рис. 2.7. Обход линии дислокации с нижнего к верхнему горизонту происходит по спирали по часовой стрелке. Для получения замкнутого контура в совершенном кристалле потребуется вектор b, который и будет являться вектором Бюргерса.
Расположение вектора Бюргерса для краевой и винтовой дислокаций различно. Для краевой дислокации вектора Бюргерса нормален к линии дислокации. Если контур Бюргерса провести вокруг винтовой дислокации, то замыкающий вектор Бюргерса окажется параллелен линии дислокации. Наиболее существенные особенности вектора Бюргерса следующие: 1) вектор Бюргерса линейной дислокации нормален к ее линии, а винтовой — параллелен ей; 2) если контур Бюргерса охватывает несколько дислокаций, то вектор Бюргерса этого контура будет равен геометрической сумме векторов отдельных дислокаций; 3) величина вектора Бюргерса вдоль линии дислокации остается постоянной; 4) вектор Бюргерса характеризует только дислокации, для других несовершенств кристаллической решетки он равен нулю.
Так как по определению контур Бюргерса проходит от атома к атому, то вектор Бюргерса в совершенном кристалле равен расстоянию между двумя атомными узлами, т.е. является вектором трансляции решетки. Дислокация, имеющая такой вектор Бюргерса, называется полной или единичной дислокацией. На рис. 2.8 показаны элементарные ячейки различных кубических решеток с векторами Бюргерса полных дислокаций. Величину и направление вектора Бюргерса записывают через его компоненты по основным кристаллографическим осям
где < hkl > - символы кристаллографического направления вектора b, a - параметр решетки. Величина вектора или так называемая мощность вектора определяется выражением (2.8) как
Отсюда для простой кубической решетки векторы Бюргерса равны:
Поэтому для простой кубической решетки полная дислокация имеет минимальный вектор Бюргерса b 1 = a [100], величина (мощность) которого равна a (a - параметр решетки). В кристаллах с ОЦК решеткой минимальный вектор Бюргерса полной дислокации характеризуется b 1 = 1/2a [111] с мощностью Если дислокация с вектором Бюргерса b 1 разделяется внутри кристалла на две дислокации с векторами Бюргерса b 2 и b 3, то должно выполняться условие
Вектор Бюргерса является важной количественной характеристикой дислокации, он определяет энергию дислокации, является мерой упругих искажений, создаваемых этим дефектом, и параметром подвижности дислокации. Как будет показано ниже, энергия дислокации пропорциональна b 2, поэтому минимальной энергией обладают дислокации с наименьшим вектором Бюргерса. Такой вектор характерен для единичной дислокации и лежит в плоскости плотнейшей упаковки, его направление совпадает с наиболее плотноупакованным направлением. Деление дислокации становится возможным, если соблюдается так называемый энергетический критерий Франка, согласно которому квадрат вектора исходной дислокации должен быть больше суммы квадратов векторов Бюргерса образовавшихся дислокаций:
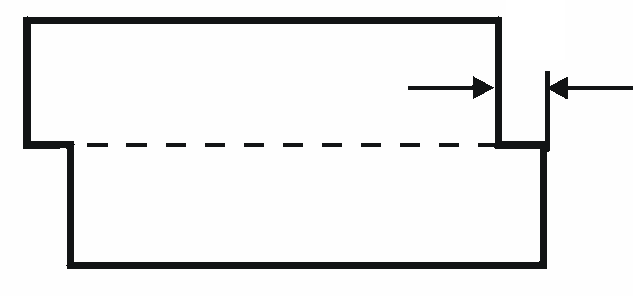
Смысл этого правила основывается на двух положениях: 1) энергия дислокации пропорциональна квадрату вектора Бюргерса, 2) дислокационная реакция должна приводить к уменьшению энергии решетки. 2.3. Движение дислокаций Движение дислокаций вызывает макроскопическую пластическую деформацию. В настоящее время можно непосредственно наблюдать движение дислокаций в тонких фольгах при помощи электронного микроскопа. Существуют два типа движения дислокаций: сдвиг (скольжение) или консервативное движение, при котором дислокации движутся в плоскости, заданной линией дислокации и ее вектором Бюргерса, и переползание или неконсервативное движение, при котором дислокация уходит из плоскости сдвига. 2.3.1. Скольжение дислокаций Пластическая деформация металлов происходит в результате сдвига в плоскостях скольжения подобно сдвигу в колоде карт. Однако такой сдвиг является конечным результатом деформации. Как показано в первом разделе при сравнении теоретической и реальной прочности кристаллов, сдвиг в плоскости скольжения кристалла не происходит одновременно, как в жесткой среде, а зарождается на каких-то участках плоскости скольжения и затем последовательно распространяется на всю плоскость. Поэтому в каждый данный момент лишь небольшая часть атомов участвует в работе против внешних сил. Механизм такого сдвига объясняется движением дислокаций. На рис. 2. 9 показаны различные положения краевой дислокации при ее скольжении под действием внешних сил. Пунктиром отмечена часть атомной плоскости, в которой уже произошел сдвиг на одно межатомное расстояние b. После выхода дислокации из кристалла, происходит полный сдвиг в плоскости скольжения одной части кристалла относительно другой, и образуется ступенька.
На рис. 2.10 показан сдвиг на одно межатомное расстояние при пробеге винтовой дислокации от передней к задней грани через весь кристалл. По мере распространения деформации на всю плоскость скольжения линия винтовой дислокации PQ будет перемещаться к заднему торцу кристалла и выйдет на него. При этом верхняя часть кристалла по отношению к нижней части сместится вправо на одно межатомное расстояние.
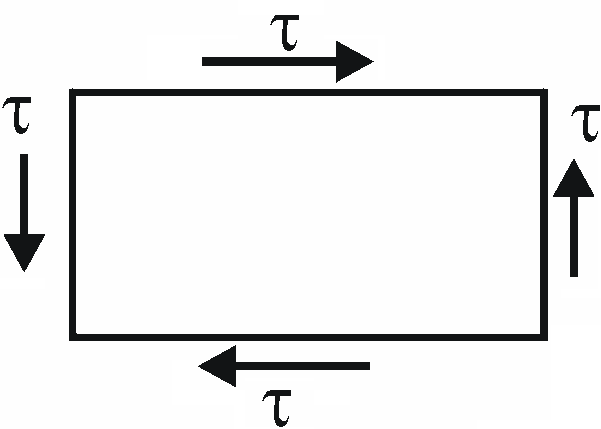
Как видно, результат аналогичен тому, что наблюдался при движении краевой дислокации, несмотря на то, что линии краевой и винтовой дислокаций расположены взаимно перпендикулярно. Эта аналогия проявляется также и в том, что касательное напряжение, двигающее краевую дислокацию, нормально к ее линии; для винтовой дислокации оно параллельно линии дислокации. Следовательно, один и тот же сдвиг при заданном напряжении может осуществиться либо винтовой, либо краевой дислокацией. Под действием одинаковых сдвигающих напряжений винтовые дислокации разного знака скользят в прямо противоположных направлениях, но сдвиг происходит в одном направлении (рис. 2.11). Особенность винтовой дислокации состоит в том, что для нее не определена однозначно плоскость сдвига. Это значит, что винтовая дислокация может скользить в любой кристаллографической плоскости, которая содержит линию дислокации и вектор сдвига. При этом в отличие от краевой, винтовая дислокация может переходить скольжением из одной атомной плоскости в другую. Если на пути движения винтовой дислокации в плоскости P встречается какой-то барьер, то дислокация начинает скользить в другой плоскости R, находящейся под углом к первоначальной плоскости скольжения P (рис. 2.11,б). Такой процесс называется поперечным скольжением. Двигаясь в новой плоскости по некоторому пути, винтовая дислокация может перейти в плоскость S, параллельную первоначальной плоскости скольжения P. В этом случае говорят о двойном поперечном скольжении. Если такой процесс повторяется многократно, то его называют множественным поперечным скольжением. Движение дислокации в плоскости скольжения называется движением скольжения или консервативным движением. Для него не требуется диффузионного перемещения атомов, и движение дислокации может происходить при низких температурах.
 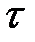 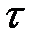
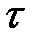
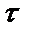
Рис. 2.11. Скольжение винтовых дислокаций; а - дислокации На рис. 2.12 на уровне кристаллической решетки схематично показано перемещение атомов при движении скольжением краевой и винтовой дислокаций. На схеме 2.12, а для краевой дислокации сплошными линиями изображены атомные плоскости до перемещения, а пунктирными — после перемещения. Атомы вдали от дислокации с обеих сторон образуют решетку с нормальным расположением атомов. Вблизи дислокации атомы симметрично смещены относительно экстраплоскости и находятся в равновесии, отвечающем некоторой минимальной энергии для этой конфигурации. Смещенные атомы с обеих сторон от дислокации стремятся занять нормальные положения, соответствующие идеальной решетке. Атомы, расположенные перед дислокацией, сдвинутые на малое расстояние, стремятся вернуться в исходное нормальное положение и препятствуют перемещению дислокации. Атомы, позади дислокации, смещенные на целый период решетки, в сдвинутой части кристалла, стремятся занять новое, нормальное положение и будут способствовать продвижению дислокации. Силы взаимодействия этих атомов равны и дислокация неподвижна. Небольшое внешнее напряжение упруго передается через нормальную решетку к уже смещенным атомам в районе дислокации и легко нарушает равновесие.
а
|

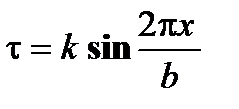
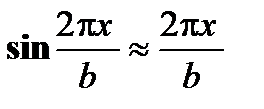 .
.
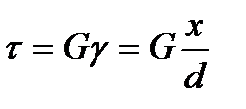 ,
,
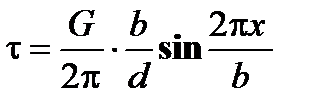 .
.
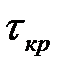 соответствует сдвигу при х=b/4, поэтому
соответствует сдвигу при х=b/4, поэтому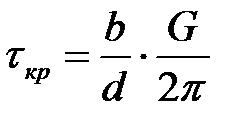 .
.
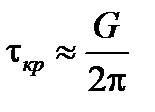 .
.

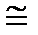 3×10‑10м) решетка сильно искажена.
3×10‑10м) решетка сильно искажена.

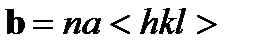 ,
,
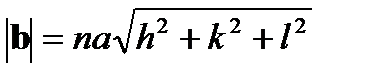 ,
,
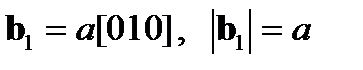 ;
;

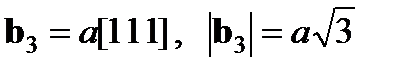 .
.

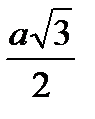 , в ГЦК b 1=1/2a [110] с мощностью
, в ГЦК b 1=1/2a [110] с мощностью 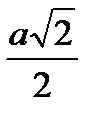 (см. рис. 2.8).
(см. рис. 2.8).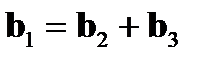 .
.
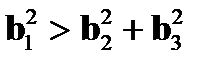 .
.