В общем случае разориентировка кристаллической решетки двух зерен и положение границы между ними определяется пятью углами или пятью степенями свободы. Такая граница называется произвольной.
Величина разориентировки двух зерен задается вектором поворота ω;, который определяет ось вращения и угол поворота θ;. Чтобы объединить два соседних зерна А и Б с получением общей решетки, необходимо повернуть одно зерно, например, Б или одновременно оба зерна вокруг вектора ω; на угол θ;. Такой поворот соответствует последовательному вращению зерна Б на углы α;, β; и γ; вокруг трех базисных векторов зерна А, дающие в совокупности поворот на угол θ;. Углы α;, β;, и γ; являются компонентами вектора поворота ω;. Отсюда, разница в угловой ориентации зерен определяется тремя числами или тремя степенями свободы.
Далее, зафиксировав относительное расположение двух зерен с заданными разориентировками α;, β; и γ;, плоскость границы можно поворачивать любым образом по отношению к двум зернам, при этом направления в зернах не изменятся. Например, если взять два разориентированных кристалла А и Б и совместить их в точке n, то через эту точку можно провести бесконечное множество плоскостей (границ), разделяющих два кристалла (зерна) (рис. 3.1). На рис. 3.1 направление [010] зерна Б повернуто относительно направления [010] зерна А вокруг направления [100] на угол α;, (вектор поворота ω; совпадает с направлением [100]). Положение границы ВE можно задать вектором EN перпендикулярным к плоскости границы и определить его ориентировку углом φ1 или φ2 относительно, например, направления [010] в зерне А (рис. 3.1 б, в). Положение границы в этом случае задается одним углом φ;, т.е. характеризуется одной степенью свободы.
Рис. 3.1. Изменение ориентировки границы относительно зерна А, а -два разориентированных кристалла, б- нормаль EN к границе ВЕ под углом φ1 к направлению [010] зерна А, в – под углом φ2 к направлению [010] зерна А.
В общем случае граница ориентирована произвольно относительно трех главных направлений [100], [010], [001] решетки. Тогда для совмещения границы с плоскостью решетки необходим поворот на два угла, поворот на третий угол является поворотом границы в собственной плоскости относительно задающего перпендикуляра и положение границы не меняет. Отсюда, ориентацию границы задают еще два угла, т. е. еще две степени свободы. Таким образом, произвольная граница характеризуется пятью степенями свободы. Иначе говоря, чтобы определить границу, надо задать пять чисел.
3.2. Классификация границ
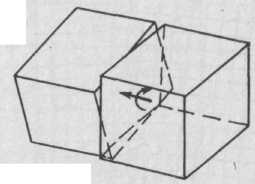
По одному из классификационных признаков границы можно разделить на границы наклона и кручения (рис. 3.2).

а б
Рис. 3.2. Границы наклона (а) и кручения (б)
Граница с вектором ω;, лежащим в плоскости границы, называется границей наклона или наклонной границей. Если вектор ω; перпендикулярен плоскости границы, то мы получим границу кручения или скрученную границу (рис. 3.2, 6). В общем случае произвольная граница смешанного типа состоит из элементов и наклона, и кручения.
По другому признаку границы с разориентировкой соседних зерен менее ~10° относят к малоугловым, а с большей разориентацией - к большеугловым (высокоугловым) границам.






