Границы кручения
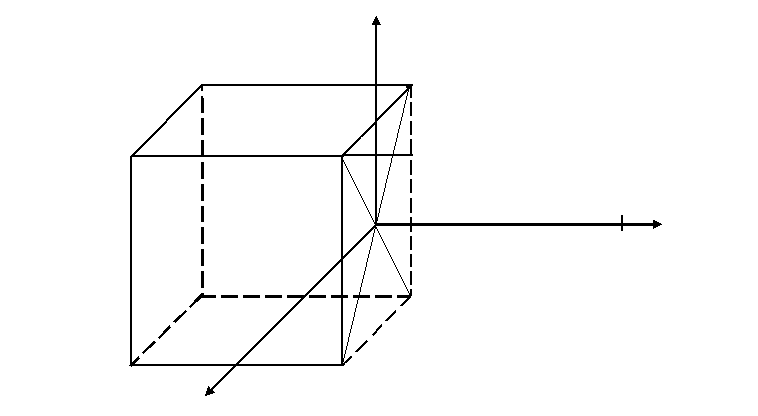
Граница с вектором ω;, расположенным перпендикулярно плоскости границы, называется скрученной границей или границей кручения. Это второй тип простейшей границы получается, если кристалл разделить плоскостью, например, (010) в той же простой кубической решетке, и одну часть вращать в этой плоскости относительно другой части вокруг направления [010]. В общем случае границей кручения может быть любая атомная плоскость, если вращать по этой плоскости одну часть кристалла вокруг нормали к выбранной плоскости. Границы кручения так же делятся на малоугловые и большеугловые (высокоугловые).
Рис. 3.15. Схема образования границы кручения
Малоугловая граница состоит из сетки двух взаимно перпендикулярных систем винтовых дислокаций, когда параллельные ряды дислокаций одной системы ортогональны параллельным рядам другой системы (рис.3.16). На рисунке 3.16 окружностями изображены атомы, лежащие над плоскостью скручивания (плоскости рисунка), а точками – под плоскостью. Особенностью малоугловой границы является наличие на плоскости закручивания больших площадей упругого сопряжения решеток соседних зерен над и под плоскостью границы с сохранением периодического строения (точки совпадают с окружностями), так же как в малоугловой границе наклона. На этих площадках решетка не прерывается при переходе через границу. Участки сопряжения разделены подстроечными, дефектными участками – винтовыми дислокациями. Вращательные компоненты деформации от дислокаций ортогональных рядов суммируются, поэтому с двух сторон от плоскости с такой сеткой дислокаций решетки будут разориентированы на небольшой угол, а сдвиговая компонента деформации, создаваемая каждой из дислокаций в ряду, компенсируется следующей дислокацией из параллельного ряда. С ростом угла кручения энергия скрученной границы растет так же, как энергия наклонной границы при увеличении угла наклона. Начинается перекрытие ядер дислокации, поэтому целесообразно перейти к модели РСУ, согласно которой минимумы энергии границы кручения должны отвечать тем углам, при которых наблюдается более или менее хорошее совпадение атомов на границе, т.е. при появлении решетки узлов совпадения. Например, поворот на 37° вокруг [001], при котором в симметричной наклонной границе в простой кубической решетке наблюдается хорошее соответствие, в границе кручения, перпендикулярной [001], также появляется совпадение атомов соседних зерен.
Рис.3.16. Малоугловая граница кручения
На рис. 3.17 изображены две границы кручения в плоскости (001) примитивной кубической решетки с углами поворота 37° и 28°, где атомы, лежащие в узлах решетки зерна ниже плоскости границы (плоскости рисунка), обозначены окружностями, а атомы выше плоскости границы черными кружками. Решетка из совпадающих узлов-кружков и узлов-окружностей, разделенных одним межплоскостным расстоянием, образуют слой элементарных ячеек, принадлежащих обоим зернам (рис. 3.17) и являющихся ячейками единой для обоих зерен решетки узлов совпадения, или когерентной решетки. Для зерен с примитивной кубической решеткой элементарная ячейка РСУ будет примитивной тетрагональной с основанием - квадрат а = b (изображен на рис. 3.17) и параметром ” с ”, равным параметру исходной ПК решетки (межплоскостному расстоянию, не изменяющемуся в параллельных скручивающихся плоскостях).
Рис. 3.17. Границы кручения в ПК решетке с углом поворота двух зерен 37° (а) и 28° (б) и решетки совпадения, имеющие соответственно
На рис. 3.18 показано образование о.ц. тетрагональной решетки узлов совпадения в ГЦК решетке при кручении вокруг вектора поворота ω;, перпендикулярного плоскости (001), на 37° в плоскости границы. Чтобы различить положение атомов в ГЦК ячейке в плоскостях, параллельных (001), на рисунке они обозначены кружками, звездочками и кубиками (рис.3.18, а). Плоскость границы условно изображена пунктиром. В горизонтальной проекции решетки на плоскость (001) (рис.3.18, б) ”кружки” и ”кубики˝, расположенные в вершинах ГЦК и по центрам горизонтальных граней, совпадают, а ˝звездочки˝, расположенные в центре вертикальных граней, находятся между ними. Проведем выше границы поворот на 37° плоскости из ˝звездочек˝ над плоскостью из ˝кружочков˝ вокруг оси [001] (рис. 3.18, в). Естественно все плоскости лежащие выше ”звездочек” также поворачиваются на 37° (на рисунке поворот этих плоскостей не изображен из-за усложнения рисунка). На рис. 3.18 (в) изображен результат поворота вокруг оси, проходящей через точку О, только плоскости из ˝звездочек˝ (над плоскостью рисунка) относительно плоскости из ˝кружочков˝ (ниже плоскости рисунка). Все ˝звездочки˝ заняли новое положение, но некоторые из них, обведенные окружностями, совпали с исходным и расположились над такими же неповернутыми под плоскостью рисунка (границы). Исходное положение нескольких звездочек (заштрихованные), которые пришли к совпадению обозначено 1, которые не совпали – 2. Решетка совпадающих узлов-звездочек изображена пунктиром. Дополнительно сплошной линией изображена решетка совпадения узлов кружков (кубиков). При повороте над плоскостью границы верхней части решетки вращаются все ее плоскости, в том числе, и следующая над ”звездочками” плоскость из ˝кубиков˝. На рис. 3.18(г) изображена горизонтальная проекция результата вращения только этой плоскости относительно плоскости из ˝кружков˝. Новое положение плоскости ”кубиков” после вращения изображено ромбами. Исходное положение нескольких ”кубиков”, пришедших (1) и непришедших (2) к совпадению обозначено квадратами. На рисунке также изображена проекция тетрагональной решетки, в вершинах которой находятся кружки (под плоскостью границы) и кубики (над границей). ”Кружки” под плоскостью границы (рисунка) и расположившиеся над ними после вращения ”кубики” образуют ячейки с основанием квадрат, изображенным на рис. 3.18(д) и третьим параметром ˝ с ˝, равным межплоскостному расстоянию (001) исходной ГЦК решетки, т.е. тетрагональные ячейки. В центрах объемов ячеек находятся ”звездочки”, пришедшие к совпадению, поэтому в целом получается ОЦТ решетка совпадающих узлов, в вершинах ячейки расположены ”кружки” и ”кубики”, а в центре - ˝звездочки˝. Эти ОЦТ ячейки непрерывно транслируются по обе стороны границы и образуют РСУ. В полученной когерентной ОЦТ решетке, наибольшую плотностью совпадающих узлов имеет плоскость {110}. Она непрерывно проходит через границу в обоих зернах и имеет индексы {210} в любой из г. ц. к. - решеток выше и ниже границы. На одну ячейку когерентной решетки, образованной поворотом на 37°, приходится десять узлов. Внутри двух горизонтальных граней ячейки находятся по четыре узла кружка и кубика, но на гранях узлы принадлежат ячейке наполовину, поэтому на когерентную ячейку из них приходится четыре узла (см. рис.3.18,г), в плоскости из звездочек пять звездочек лежат целиком внутри ячейки (см. рис.3.18, в) и один вершинный узел. Итого десять узлов приходится на всю ячейку РСУ решетки: девять – внутри ячейки и один – вершинный. Из них два узла приходятся на когерентную ячейку, поэтому доля узлов РСУ в общем количестве узлов, входящих в ячейку после кручения в ГЦК решетке на 37°, составляет 1:5. Как видно из рис.3.18, 1 и 2 поворот на 37° приводит к появлению в кубических ПК и ГЦК решетках к образованию РСУ с Σ=5. Такой же результат появится и для ОЦК решетки. Учитывая высокую симметрию кубических решеток, каждую когерентную решетку можно получить несколькими различными поворотами относительно различных осей. Некоторые углы поворота в ГЦК и ОЦК решетках, приводящие к получению одинаковых РСУ, приведены в таблице 3.2.
а б в г
д
Таблица 3.2. Характеристики некоторых решеток совпадения в
Задачи Задача 1. Расположите элементы Al, Nb, Ni и Sn в ряд в порядке предположительного возрастания энергии образования вакансий. Дайте необходимые пояснения. Решение: Энергии образования вакансий Ео можно приближенно оценить по энергии активации самодиффузии
Ответ: Sn→Al→Ni→Nb.
Задача 2. При температуре вблизи точки плавления равновесная концентрация вакансий в магнии равна 7,2·10-4. Приближенно оцените равновесную концентрацию вакансий в магнии при комнатной температуре. Решение: Для магния Ответ: 1,22∙10-10.
Задача 3. Приближенно оцените энергию образования вакансии в ГЦК металле, если экспериментально определенная равновесная концентрация вакансий при 927 °С равна 1∙10-5. Решение: Т.к. Ответ: 1,2 эВ.
Задача 4. Оцените, на сколько порядков изменится равновесная концентрация вакансий в золоте при повышении температуры с 600 до 1000 °С, если при 600 °С эта концентрация равна 9,1∙10-6. Решение: Т.к. Отсюда Ответ: 3,5∙10-4.
Задача 5. В меди, закаленной с 600 °С, содержится 1,1∙10-5 % (ат.) вакансий. Какую температуру закалки следует выбрать, чтобы концентрация вакансий возросла на два порядка? Решение: Т.к.
Ответ: ~950°С.
Задача 6. Металл содержит равномерно распределенной примеси замещения. Определите среднее расстояние между примесными атомами в единицах периода ГЦК. и ОЦК. решетки. Решение: С=0,1 ат.%=10-3. Для примитивной решетки (1 атом на 1 элементарную ячейку) примесь замещения повторяется через 10 периодов решетки, т.е через lприм = 10а. Т.к. к ГЦК 4 атома на 1 элементарную ячейку, а а ОЦК – 2, то lГЦК = 10а / Ответ: 6,3 и 7,9 a.
Задача 7. Экспериментальные определения относительной концентрации вакансий в меди дали значения 8∙10-5 при 980° С и 16∙10-5 при 1060°С. По этим данным рассчитайте энергию образования и энтропию образования вакансии в меди. Решение: Т.к.
Прологарифмируем оба уравнения и вычтем из первого второе. Отсюда получим Энтропия Ответ: 0,81 эв и -1,3k
Задача 8. У кристалла закиси железа FехО постоянная решетки a = 4,30 Å, а плотность равна 5,72 г/см3. Каков состав кристалла (т. е. значение в формуле FexO)? Определите ваши предположения о структуре этого кристалла. Решение: FехО имеет решетку типа NaC l, a = 4,30 Å=0,43 нм. На 1 элементарную ячейку приходится по 4 иона Fe и O. При составе FeO плотность
Ответ: x=0,94. Задача 9. Кристалл вюстита (приблизительный состав FexO) имеет структуры типа NaCl и содержит 76,08 вес.%. Было найдено, что его плотность равна 5,613 г/см3, а период решетки a=4,2816Å. Содержит ли этот кристалл вакансии по железу или межузельные ионы кислорода? Какова плотность вакансий (или межузельных атомов)? Решение: При составе FeO вес.% Fe равен 55,85/(55,85+16)=0,7773 или 77.73 вес.%. Т.к. ρ<ρ0 (см.пред. задачу), кристалл содержит вакансии по Fe (т.к. rFe+2 < rO-2), а не межузельные ионы кислорода. Нехватка ионов Fe составляет n = (77,73-76,08)/77,73 = 0,0212 или 2,12%.Т.е состав FexO – Fe0,98O. В 1 элементарной ячейке по 4 иона Fe, т.е. нехватка ионов Fe (или доля вакансий по Fe) на 1 элементарную ячейку равно 4n=0,0848. Плотность вакансий по Fe составляет 4n/a3 = 0,0848/4,28168 ∙10-24 см3= 6,2∙1021 см-3. Ответ: плотность вакансий по железу 6,2∙1021 см-3.
Задача 10. Если концентрация вакансий в алюминии при его температуре плавления составляет 9,4∙10-4 и если после закалки алюминия от температуры плавления вакансии конденсируются в диски на плотно упакованных плоскостях и образуют петли Франка, определите плотность создающихся дислокаций при радиусе петель а) 50 Å и б) 500 Å. Решение: Если концентрация вакансий n =9,4∙10-4, а параметр решетки алюминия a =4,05∙10-8 см, то петли Франка образуются в плотноупакованной плоскости (111) с межплоскостным расстоянием d111 = a / Ответ: 1,3∙1011 см-2 и 1,3∙1010 см-2.
Задача 11. Стержень из золота нагревается до температуры плавления, при которой концентрация вакансий составляет 7,2·10-4 от числа узлов решетки. Затем этот стержень закаливают так, что все вакансии, генерированные при температуре плавления, оказываются захваченными в металле. Если отжигать этот стержень при постоянной, чуть более высокой температуре, то наблюдается сокращение его размеров по мере уменьшения концентрации вакансий до ее равновесного, очень низкого значения. Если величина всего сжатия равна 1,1∙10 -4, то какова будет величина изменения параметра решетки в процессе этого отжига? Решение: Концентрация вакансий nв/N=7,2·10- 4, сжатие ΔV/V=1,1∙10 -4. Изменение длины стержня ΔL/L=1/3 ∙ ΔV/V. При нагревании изменение длины ΔL/L связано как с появлением вакансий в объеме, так из-за изменения параметра решетки Δa/a: ΔL/L=nв/3N + Δa/a. Отсюда относительное изменение параметра решетки Δa/a = ΔL/L-1/3 ∙ nв/N = (1,1-7,2/3)·10-4=-1,3·10-4. Т.е. параметр решетки уменьшается при нагреве и растет при охлаждении. Ответ: относительное увеличение = 1,3∙10-4. Задача 12. Оценить равновесную концентрацию вакансий в серебре в точке плавления 961 °С, зная модуль сдвига G = 2,8∙103 кгс/мм2 и период решетки а = 4,078 Å. Решение:
Ответ: 0,52·10-4.
Задача 13. В поликристалле зерно размером d = 10 мкм содержит избыток вакансий 1∙10-4. Оценить перемещение Δх границ, если все вакансии стекут на границы. Решетка ГЦК с периодом a =4·10-8 см. Считать зерно шаром. Решение: Объем шара V=4/3 πR3=1/6 πd3. Изменение объема шара связано с избытком вакансий и Ответ: 0,13 a
Задача 14. Резкая закалка меди от точки плавления может уменьшить ее плотность на 0,02 % за счет увеличения концентрации вакансий. При какой относительной и абсолютной погрешности измерений длины и массы (или силы) это изменение можно надежно обнаружить: а) прямым измерением плотности; б) гидростатическим взвешиванием. Перечислить побочные источники ошибки при этих измерениях. Решение: Дано Δρ/ρ0=0,02 %=2·10-4. а) Прямым измерением плотности. Т.к. масса образца не меняется, то меняется его объем (размеры) и Δρ/ρ0~3 ΔL/L. При точности 10% относительная погрешность определения длины ΔL/L=1/3 ·1/10 · Δρ/ρ0 = 0,7·10-6 или 0,00007%. При бесконтактном измерении длины (чтобы не смять образец) ошибка должна быть не менее длины волны ΔL~λ=0,6 мкм. При ΔL/L=0,7·10-6 длина обраца должна быть не менее L = ΔL/0,7·10-6= 0,6 мкм/0,7·10-6=0,85·106 мкм = 0,85 м. Побочные источники ошибок: 1 ΔТ, т.к. из-за колебания температуры и т.к.р. изменяется размер; 2 Размер печи и секционное регулирования Т; 3 Чистота образца не хуже 99,999%, чтобы не было из-за испарения примесей; 4 Исключить прогиб образца, он должен лежать на теплопроводящей плите из инертного материала; 5 Отсутствие поглощения газов, нагрев в инертной атмосфере специальной очистки. б) Гидростатическим взвешиванием. Изменение плотности по изменению веса (силы). Относительная погрешность определения силы ~ 0,002 % при точности 10%. При взвешивании с погрешностью ±1 мг вес образца должен быть не менее 1 мг/ 2·10-5 = 0,5 кг.
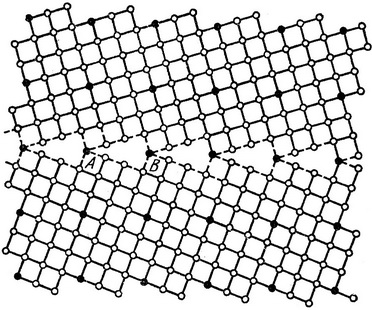
Задача 15. Вектор Бюргерса дислокации b в металле обычно совпадает с кратчайшим вектором трансляции, а плоскость скольжения Р — с плоскостью плотнейшей упаковки. Перечислить возможные системы скольжения в решетке ГЦК. (Считать + b и - b за один вектор). Решение: В ГЦК решетке плоскость плотнейшей упаковки – {111}. Направление с кратчайшим вектором трансляции (вектор Бюргерса) – ½ <110>. Для каждой из четырех различно ориентированных плоскостей {111} – (111), (Τ11), (1Τ1), (11Τ) из шести направлений скольжения <110> имеется по три направлений скольжения. Например в плоскости (111) - вектор Бюргерса b = ½ a [0IĪ] или ½ a [Ī0I] или ½ a [101]. В ГЦК решетке все семейства скольжения одинаковы - семейство скольжения <110>{111}, которое (если считать + b и - b за один вектор) содержит 12 систем скольжения – по 3 вектора Бюргерса в каждой из 4 плоскостей сколжения.
Задача 16. В решетках с неплотной упаковкой скольжение часто возможно по плоскостям нескольких семейств с наиболее плотной упаковкой. В a-железе работают первые три из числа наиболее плотноупакованных плоскостей, содержащих вектор Бюргерса. Перечислить семейства скольжения в a-железе. Указать число систем скольжения в каждом семействе.
Рис. 4.1. К задаче 16. Плоскости и направления скольжения в a-Fe:
Решение: в a-Fe скольжение идет вдоль направления <111>, которое соответствует наименьшему для полной дислокации вектору Бюргерса b =0,5a[111]. Плоскость {110} – наиболее плотноупакованная, а плоскость {112} – главная плоскость дефекта упаковки. Скольжение в плоскости {123} проявляется при высоких температурах или при малых скоростях деформации и любых температурах. Для каждого из 4-х направлений скольжения типа <111> расположено по 12 плоскостей, входящих в совокупность {110}, {112} и {123}, образуя 48 систем скольжения. Задача 17. Показать, что дислокация не может обрываться внутри кристалла. (Указание: Предположим, что дислокация обрывается внутри кристалла. Прямоугольный контур Бюргерса, составленный из ребер призмы, будет замкнут на всех поверхностях, через которые дислокация не проходит; на поверхности, через которую дислокация входит в призму, контур будет не замкнут. Показать, что в этом есть противоречие.) Решение:
Если дислокация кончается в точке С, то обходя по плоскости скольжения вокруг тоски С (из зоны, где сдвиг b прошел, в зону, где его не было) мы пересекаем какую-то линию разрыва смещения b, т.е. такую же дислокацию. Поэтому дислокация либо образует замкнутый контур, либо заканчивается на некоторой поверхности – границе зерна или границе фаз.
Задача 18. Вектор Бюргерса дислокационной петли одинаков во всех точках. Означает ли это, что и характер дислокации одинаков во всех участках петли? Решение: Дислокацию кроме вектора Бюргерса b характеризуется еще вектором оси (или линией дислокации) l. Таким образом, дислокация – тензорный объект. Линия дислокации – это граница зоны сдвига, всегда замкнутая линия. В общем случае в плоскости скольжения линия дислокации – кривая. Отдельные малые части этой кривой имеют разную ориентацию линии дислокации l и направления сдвига b, такая дислокация называется смешанная, с разной долей составляющих краевой и винтовой компонентов.
Задача 19. Оценить (в километрах) суммарную длину всех дислокаций в 1 см3 отожженного металла с плотностью дислокаций 108 см-2. Решение: Плотность дислокаций ρд =108 см-2, объем металл V =1 см3. Т.к. ρд=Σlд / V, то суммарную длину всех дислокаций Σlд=Vρд = 1 см3 ∙ 108 см-2 = 108 см = 1000 км. Ответ: 1000 км
Задача 20. Устойчив или неустойчив ряд параллельных винтовых дислокаций в плоскости скольжения? Решение: Решетка вокруг винтовой дислокации испытывает чисто сдвиговую деформацию. На расстоянии r от оси дислокации касательное напряжение Знак (+) соответствует параллельным (одноименным) дислокациям – взаимное отталкивание. Знак (-) соответствует антипараллельным (разноименным) дислокациям - взаимное притяжение (до аннигиляции).
Задача 21. Рассмотрите взаимодействие между двумя краевыми дислокациями с параллельными плоскостями скольжения в кристалле меди, если одна из дислокаций закреплена. Определить силы скольжения и переползания при х= 70 Å и у =30 Å. Решение: При х =70 Å и у =30 Å и параметре решетки меди a =3,61 Å, G =4,55 · 1010 Н/м2, μ;=0,35. Межатомное расстояние равно |b|= a /
Сила переползания на единицу длины
Ответ: 6,07∙10-7 Н/мм и 1,02 · 10-6 Н/мм.
Задача 22. Докажите, что сила взаимодействия параллельных краевой и винтовой дислокаций равна нулю.
Решение: В решетке ГПУ чередование плотноупакованных слоев при нарушении укладки будет следующим:
Дефект укладки создает прослойку с чередованием слоев АВСА, свойственную для 3-х слойной ГЦК решетки. Вне этой прослойки чередование слоев характерно для 2-х слойной ГПУ решетки - … АВАВ …
Задача 24. Оцените критическое напряжение течения для меди с равномерно распределенными в ней сферическими частицами SiO2 радиусом 10 нм при объемной доле этих частиц, равной 0,1%. (Модуль сдвига G для меди равно 42,4 кН/мм2). Решение: Радиус сферических частиц r=10 нм c объемной долеq этих частиц f =0,1%=10-3. Для меди a =0,361 нм, G =42,4 кН/мм2. В ГЦК решетке b = a λ=D(π/6f) τкр=τо+Δ τдисп= G/30 + Gb/ λ; = G ∙ 0,60 = 25,5 кН/мм2. Ответ: 25,5 кН/мм2.
Задача 25. Оценить минимальное число дислокаций, пробег которых через кристалл никеля приводит к образованию ступеньки на поверхности кристалла, различимой в световом микроскопе. (Период решетки никеля a =0,352 нм, разрешение светового микроскопа — около 0,25 мкм). Решение: Для никеля a =0,352 нм, Δl =0,25 мкм. В ГЦК решетке b = a Ответ:
Задача 26. Оценить температуру конденсации атмосфер Коттрелла в железе с 0,01 % (по массе) N, если энергия взаимодействия краевой дислокации с атомом азота U = 0,5 эВ. Как изменится эта температура после очистки железа до 0,001 % (по массе) Ν;? Решение: Для С1 =0,01 % (по массе)=10-4, С2 =0,001 % (по массе)=10-5, Е =0,5 эв. Температуру конденсации атмосфер Коттрелла Тк=Е/k lnC-1, т.к. C= C1exp(-E/kT). Для С1=0,01 % (по массе)= 0,01 ат.% (АFe/АN)= 0,01 ат.% (55,85/14) = 0,0399 ат.%. Отсюда Тк1=0,5∙1,6∙10-19 дж / 1,38∙10-23 Дж/К ln C1-1=741 oK = 468 oC. Аналогично, для С2=0,001 % (по массе) Тк2 = 572 oK = 299 oC ≈ 300 oC. Ответ: 468 oC и 300 oC.
Задача 27. Оценить величину слоя конденсации атмосфер при полном осаждений на дислокациях всего углерода из мартенсита с 0,20% С, если плотность дислокаций ρ;=1012 см-2. Какой концентрации углерода достаточно для получения сплошной одноатомной цепочки углерода на всех дислокациях? Решение: В a-железе параметр решетки равен a =0,2866 нм = 0,2866 ∙ 10-7 см. Сплошная одноатомная цепочка на всех дислокациях при конденсации атомов углерода образуется при концентрации углерода в атомных долях С= ρд a2 = 1012 см-2 ∙ 0,28662 ∙ 10-14 см2 = 8,2 10-4 = 8,2 10-2 ат.% = 8,2 10-2 (АN/АFe) % (по массе) =8,2 10-2 ∙(12/55,85) = 1,8 10-2 % (по массе). При осаждений 0,20 %С величина слоя составит 0,20% / 0,018% ≈ 11 атомных слоев. Ответ: 1,8 10-2 % (по массе) и ≈ 11 атомных слоев углерода.
Задача 28. Начертите и определите структуры решеток совпадения, получающихся в ОЦК-решетке при повороте на 36,9° вокруг оси (100). Решение: В ОЦК решетке при повороте на φ;=36,9о вокруг оси (100) степень несовпадения узлов Σ=5. При таких спецориентировках может возникнуть «сверхрешетка», общая для обеих зерен (темные атомы). Узлами такой «сверхрешетки» в плоскости границы будут атомы А и В. Общие для обеих зерен. Для описания таких границ вводится объемная решетка совпадающих узлов (РСУ). Размер ячейки РСУ характеризуется параметром:
а) укажите, что представляет собой плоскость границы; б) какова суммарная длина дислокаций на единицу площади этой границы? в) вычислите угол, при котором индивидуальные дислокации, составляющие границу, становятся неразличимыми; Решение: Для ГЦК решетки а = 4 Å угол разориентировки φ;=1/2°=0,0087 рад. а) Плоскость границы – плоскость типа {110}; б) Связь угла разориентировки φ и расстоянием между дислокациями D в малоугловой симметричной наклонную границе b /2= D sin φ;, или при малых углах D= b/φ;.
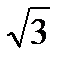 /2∙ a = /2∙ a = 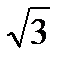 /10 рад ≈ 9,9°. /10 рад ≈ 9,9°.
Ответ: а) {110}; б) 3,1∙105 см-1; в) ≈8о.
Задача 30. Два кристалла имеют простую кубическую решетку с периодом a и общую ось [100]. На ячейку решетки совпадений приходится Σ = 5 узлов кристаллической решетки. Граница проходит по плоскости (010) решетки совпадений. При отклонении зерен от этого положения появляются зернограничные дислокации. В каком диапазоне углов разворота решеток шаг этих дислокаций будет не менее 20 a? Решение: Для простой кубической решетки b = а. Связь угла разориентировки φ; и расстоянием между дислокациями D в малоугловой симметричной наклонную границе b /2= D sinφ, или при малых углах sinφ≈φ и D=b/φ;. Отсюда ±Δω=φ= b/D = а / 20а = 0,05 рад = 2,86о. Ответ: 2,86о
Задача 31. Определите кристаллографические индексы плоскости, в которой находится симметричная малоугловая граница наклона в никеле.
Ответ: Плоскость типа {110}
Задача 32. Определите расстояние между дислокациями в симметричной малоугловой границе наклона в никеле, если угол разориентировки субзерен равен 12'. Решение: Для никеля a =0,352 нм. В ГЦК решетке b = a
|



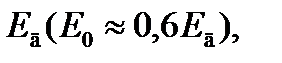 которая приближенно пропорциональна Тпл. Поэтому ряд в порядке предположительного возрастания энергии образования вакансий:
которая приближенно пропорциональна Тпл. Поэтому ряд в порядке предположительного возрастания энергии образования вакансий: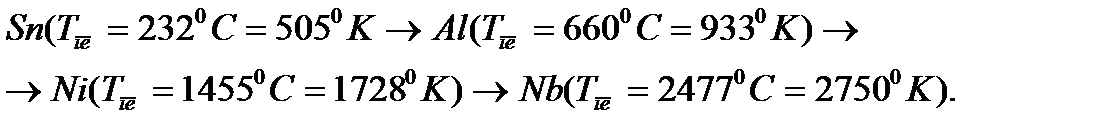
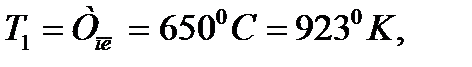
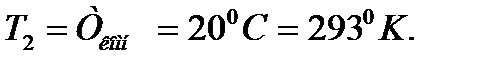 При температуре вблизи точки плавления С1=7,2·10-4. Равновесную концентрацию вакансий при комнатной температуре С2. Т.к.
При температуре вблизи точки плавления С1=7,2·10-4. Равновесную концентрацию вакансий при комнатной температуре С2. Т.к.  то
то  Отсюда
Отсюда 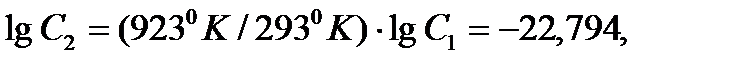 а C2=1,22∙10-10.
а C2=1,22∙10-10.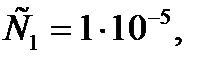
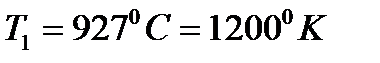 и
и  то
то 

 и
и  а C2=3,5∙10-4.
а C2=3,5∙10-4.
 а
а и
и 
 =6,3а, lОЦК = 10а /
=6,3а, lОЦК = 10а /  = 7,9а
= 7,9а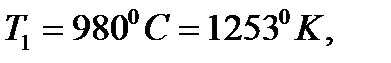

 и система двух уравнений с двумя неизвестными - энергия образования Eo и энтропию образования S вакансии:
и система двух уравнений с двумя неизвестными - энергия образования Eo и энтропию образования S вакансии: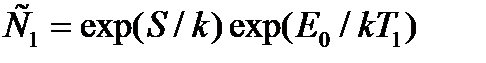

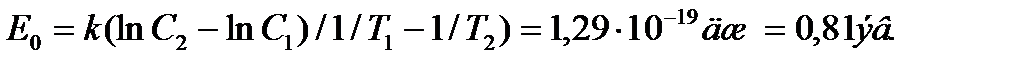
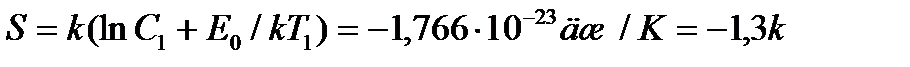
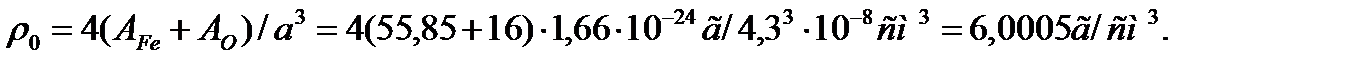
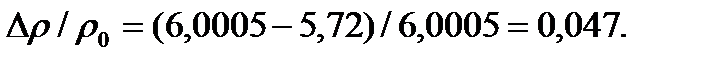 Часть позиций ионов Fe+2 – вакансии, и формула закиси железа FexO. Найдем значение x их выражения (55,85+16)/(55,85+16)=1-0,047. Отсюда x=0,94.
Часть позиций ионов Fe+2 – вакансии, и формула закиси железа FexO. Найдем значение x их выражения (55,85+16)/(55,85+16)=1-0,047. Отсюда x=0,94. . При радиусе петли R1=50 Å=50∙10-8 см объем вакансионного диска V1=πR12d111, а длина петли L1=2πR1. При этом объем всего металла V0=V1/n. Отсюда плотность дислокаций ρ1=L1/V0=2n/R1d111 = 2∙9,4∙10-4∙
. При радиусе петли R1=50 Å=50∙10-8 см объем вакансионного диска V1=πR12d111, а длина петли L1=2πR1. При этом объем всего металла V0=V1/n. Отсюда плотность дислокаций ρ1=L1/V0=2n/R1d111 = 2∙9,4∙10-4∙ 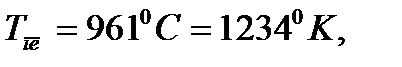
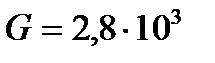 кгс/мм2 = 28∙103 Н/мм2, а =4,078 Å=4,078·10-7 мм. Энергия образования вакансии Ев=αвGb3, где αв ≈1/4. Вектор Бюргерса полной дислокации а /2 <110> в ГЦК решетке равен b = а /
кгс/мм2 = 28∙103 Н/мм2, а =4,078 Å=4,078·10-7 мм. Энергия образования вакансии Ев=αвGb3, где αв ≈1/4. Вектор Бюргерса полной дислокации а /2 <110> в ГЦК решетке равен b = а /  .Отсюда Ев = 1,678·10-19 Дж = 1,05 эВ. Равновесную концентрацию вакансий в серебре в точке плавления
.Отсюда Ев = 1,678·10-19 Дж = 1,05 эВ. Равновесную концентрацию вакансий в серебре в точке плавления .
.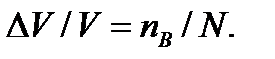 Изменение объема шара
Изменение объема шара  Отсюда
Отсюда 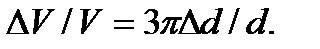 Отсюда перемещение границ Δх= Δd/2= nв/N d/6π = 0,53·10-4 мкм = 0,53·10-8 см. Т.к. a =4·10-8 см, то Δх =0,13 a
Отсюда перемещение границ Δх= Δd/2= nв/N d/6π = 0,53·10-4 мкм = 0,53·10-8 см. Т.к. a =4·10-8 см, то Δх =0,13 a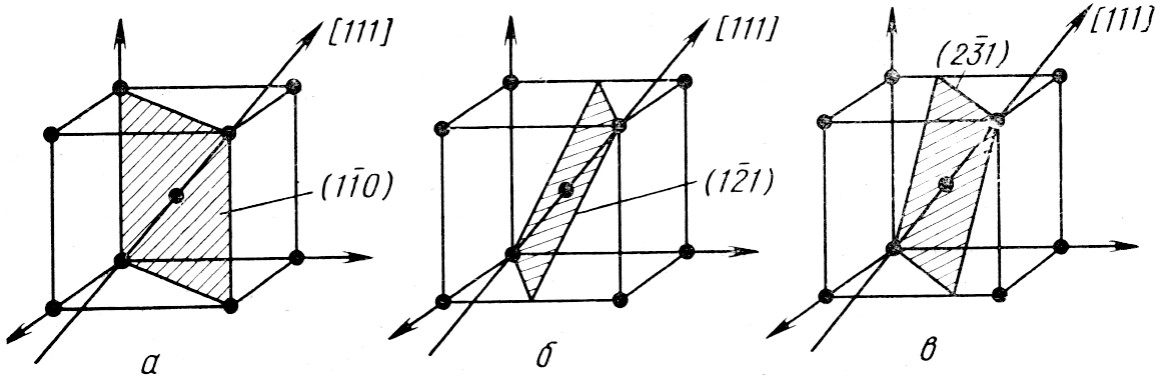
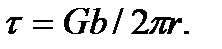 Две параллельных винтовых дислокации действуют друг на друга с силой
Две параллельных винтовых дислокации действуют друг на друга с силой 
 = 237 Н/мм2. Сила скольжения на единицу длины
= 237 Н/мм2. Сила скольжения на единицу длины
 = 0,022 G, Å = 1,02 · 10-6 Н/мм.
= 0,022 G, Å = 1,02 · 10-6 Н/мм.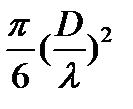 , отсюда
, отсюда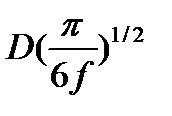 . Критическое напряжение течения
. Критическое напряжение течения 103.
103. Σ=(объем ячейки РСУ) / объем исходной ячейки = 5.
Σ=(объем ячейки РСУ) / объем исходной ячейки = 5. Т.к. b = a
Т.к. b = a 


