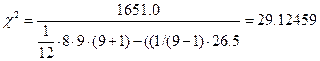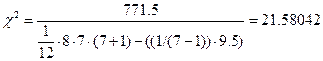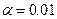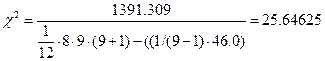Расчет коэффициента конкордации W
Результаты расчета коэффициентов Т, как и расчеты «связанных» рангов, приведены в Приложении 1. Пример расчета коэффициентов Т и S для начальника отдела: S1=(28,5-624/12)2=552,25 S2=(18,5-624/12)2=1122,25 S3=(37,0-624/12)2=225,0 S4=(52,5-624/12)2=0,25 S5=(58,5-624/12)2=42,25
T1=((33-3)*2+(23-2)*2)*1/12=5 T2=((33-3)+(23-2)*3)*1/12=3,5 T3=((33-3)*2+(23-2)*2)*1/12=5 T4=((33-3)+(23-2)*3)*1/12=3,5
Расчет коэффициента конкордации W для сотрудников: Начальник отдела:
Программист:
Инспектор:
Социолог:
Когда мнения специалистов полностью совпадают, то W=1, при несовпадении W=0, т.е. 0£W£1. При решении задач данного класса достаточным для вывода о согласованности мнений экспертов можно принять значение W³0,4. В данном случае мнения экспертов согласованы, так как значения коэффициентов конкордации достаточно высоки, следовательно, не требуется проведения более точного обследования. Для оценки значимости коэффициента конкордации W используется критерий c2 (“хи-квадрат”), который подчиняется c2 распределению с числом степеней свободы n-1=f:
Расчет значения критерия c2для сотрудников Начальник отдела: Число степеней свободы: 12-1=11
С вероятностью Р=0,999 можно считать, что мнение экспертов не случайно. Программист: Число степеней свободы: 9-1=8
c2табл =26,1 С вероятностью Р=0,999 можно считать, что мнение экспертов не случайно. Инспектор: Число степеней свободы: 7-1=6
c2табл =16,81 С вероятностью Р=0,99 можно считать, что мнение экспертов не случайно. Социолог: Число степеней свободы: 9-1=8
c2табл =20,1 С вероятностью Р=0,99 можно считать, что мнение экспертов не случайно.
|
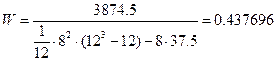
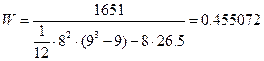
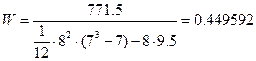
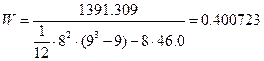
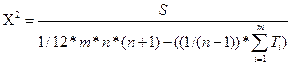
Если c2расч >c2табл для соответствующего числа степеней свободы, то с вероятностью p можно считать, что мнение экспертов неслучайно.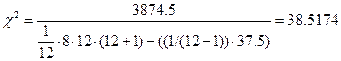
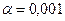c2табл =31,3
