Лінійна залежність і лінійна незалежність системи векторів
Означення 1. Система векторів
за умови, що хоча б один з коефіцієнтів Якщо система векторів лінійно залежна, то хоча б один з них можна подати у вигляді лінійної комбінації інших. Дійсно, якщо, наприклад,
Навпаки, якщо
то вся система
де Означення 2. Система векторів
тільки за умови рівності нулю всіх коефіцієнтів Поняття лінійної залежності векторів дозволяє характеризувати їх взаємне положення в просторі. Теорема 1. Два вектори лінійно залежні тоді і тільки тоді, коли вони колінеарні. Теорема 2. Довільні три вектори лінійно залежні тоді і тільки тоді, коли вони компланарні. Теорема 3. Чотири вектори завжди лінійно залежні, тобто існують числа
Зауваження. Розклад (2) за системою трьох некомпланарних векторів Дійсно, якщо припустити, що існує ще один розклад:
то віднімаючи із (2) останню рівність, отримаємо:
Оскільки
Приклад. Накресліть довільний базис
|
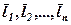називається лінійно залежною, якщо їх лінійна комбінація дорівнює нульовому вектору: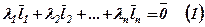
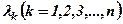відмінний від нуля.
, то з (1) випливає:
;
лінійна комбінація векторів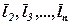 
, тобто
,
.
.
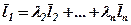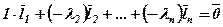
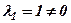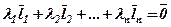
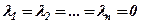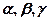такі, що для векторів 
має місце співвідношення: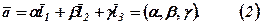
- єдиний.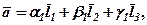
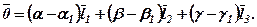
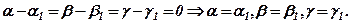
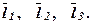Побудуйте вектори 
, 
, 
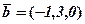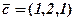і 
