Базис. Декартові система координат. Дії над векторами в координатній формі
Означення. Система лінійно незалежних векторів простору, за якими можна розкласти довільний вектор, називається базисом цього простору. Так з теореми 3 випливає, що довільні три некомпланарні вектори Будемо вважати, що базисні вектори Означення. Сукупність базісу Іноді таку систему називають косокутною. Числа
Аналогічно, на площині базис утворюють всякі два неколінеарні вектори, а всякий компланарний з ними може бути розкладений за цим базисом. Базисним вектором на прямій лінії може бути всякий ненульовий вектор. Із властивостей лінійних операцій над векторами випливає, що при додаванні і відніманні векторів в даному базисі додаються і віднімаються їх відповідні координати, а при множенні вектора на число множаться на це число координати вектора, тобто
Вектори рівні, коли вони мають рівні відповідні координати. Приклад. У деякому базисі задані своїми координатами вектори Розв’язання. Розклад вектора
де числа
(2 (2 За властивістю 30 про рівність векторів отримаємо систему рівнянь
Отже,
|

 утворюють в тривимірному просторі базис, за яким, згідно з формулою (2) і зауваження до неї, можна єдиним чином розкласти довільний вектор
утворюють в тривимірному просторі базис, за яким, згідно з формулою (2) і зауваження до неї, можна єдиним чином розкласти довільний вектор 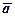 простору. Вектори
простору. Вектори 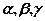 , про які згадувалось у 2.3, називають координатами вектора у заданому базисі, пишуть:
, про які згадувалось у 2.3, називають координатами вектора у заданому базисі, пишуть: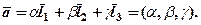
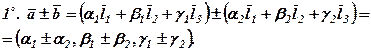
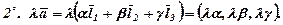
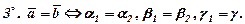
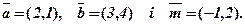 Розкласти вектор
Розкласти вектор  за базисом, який утворений із векторів
за базисом, який утворений із векторів 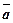 і
і  .
.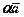 + β;
+ β;  і β – невідомі. Щоб їх знайти підставимо в останню рівність координати векторів
і β – невідомі. Щоб їх знайти підставимо в останню рівність координати векторів 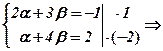 -5β = -5, β = 1, ά = -2.
-5β = -5, β = 1, ά = -2.


