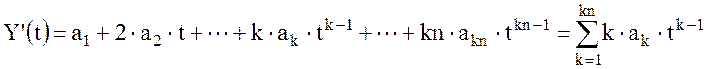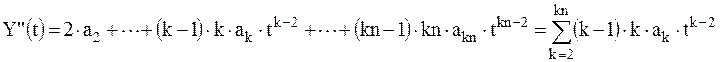Выбор метода аппроксимации исходных данных
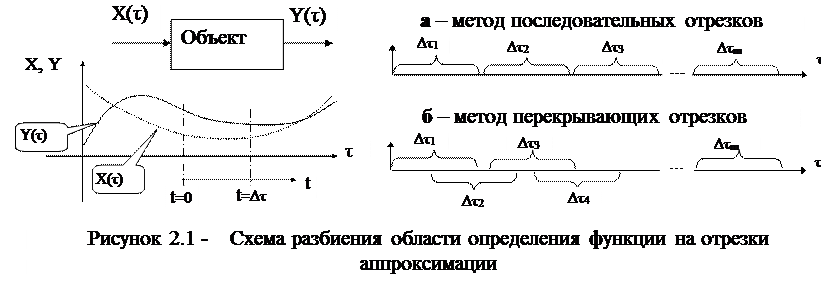
Вся область изменения величин f(x) и y(x) разбивается на отрезки оси времени, которые могут перекрывать следовать друг за друга (Рис.2.1а) или перекрывать друг за друга (Рис.2.1б).
На каждом интервале (индекс интервала - nz) используется локальная в пределах каждого интервала независимая переменная – t.
Зависимости X(t) и Y(t) в пределах каждого интервала аппроксимируются подходящими функциями (например, полиномами невысоких степеней):
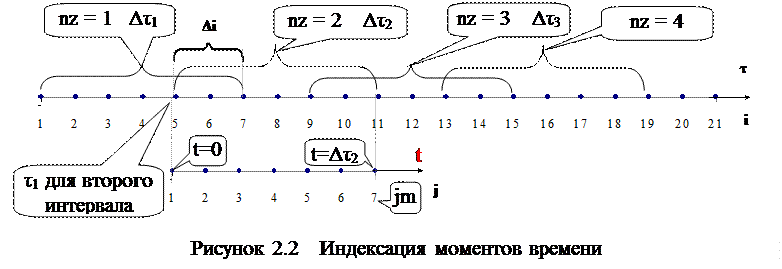
где τ – независимая переменная; i – индекс момента времени на оси основной независимой переменной τ; Δτ - отрезок времени на котором проводится аппроксимация; t = τ-τ1 - локальная (в пределах nz отрезка) координата времени; τ1 – момент времени соответствующий началу отрезка; j – индекс момента времени на вспомогательной оси независимой переменной t (в пределах локального отрезка времени); jm – индекс момента времени конца отрезка (на вспомогательной оси t); nz – индекс отрезка времени; Δi – количество узловых точек входящих в зону перекрытия отрезков; а0 ¸ аnf и b0 ¸ bmf - коэффициенты аппроксимирующих полиномов; nf, mf - порядки аппроксимирующих полиномов. Таким образом для аппроксимации представляются данные в табличном виде:
Выбранный способ представления данных для проведения аппроксимации экспериментальных зависимостей X(τ) и Y(τ) отличается тем, что он не требует равномерного расположения моментов времени на оси τ. Другим достоинством принятого способа является возможность существенного перекрытия интервалов времени при аппроксимации, что заметно повышает достоверность результатов идентификации. Представляется разумным использовать максимальное перекрытие интервалов когда Δi = jm-1. Так реализуется метод скользящих отрезков.
|

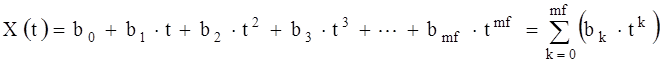
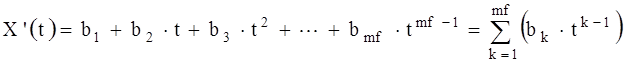
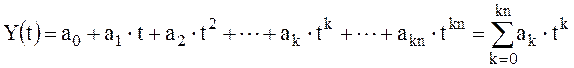 (2.5)
(2.5)