Методика аппроксимации экспериментальных данных
Аппроксимация табулированных экспериментальных данных на отрезках оси времени проводится с используются полиномов невысоких порядков. Рассмотрим в качестве аппроксимирующей функции f(t) полином степени n
где t - локальная (в пределах nz отрезка) координата времени; n – порядок полинома. Будем минимизировать d - сумму квадратов невязок (рассогласований значений заданной и аппроксимирующей функций) во всех jm точках отрезка времени
где f – значение аппроксимируемой табулированной функции; f(t,a) - значение аппроксимирующей функции (полином); j - – индекс момента времени. Согласно теории необходимым условием минимума функции d является равенство нулю ее частных производных
Развернув (2.8) получаем систему уравнений (2.9) для определения коэффициентов аппроксимирующего полинома a0, a1, a2,…,an.
Путем формальных преобразований система уравнений (2.9) приводится к системе линейных алгебраических уравнений (СЛАУ) (2.10) с матрицей Грамма вида:
Для формирования матрицы Грамма можно использовать процедуру Gram(N,A,X,Y,M,K). Решение полученной СЛАУ можно проводить прямым методом Гаусса с выбором главного элемента с использованием процедуры Gauss(M, A, X, S). (2.11) При проведении аппроксимации в среде Excel можно использовать линию тренда как показано на рис.2.4
Оценку эффективности аппроксимации можно проводить визуально, но лучше использовать оценку R2. Желательно получать величину R2 как можно ближе к 1. Для этого необходимо менять порядок аппроксимирующего полинома. Проведя дифференцирования полученного выражения для аппроксимирующего полинома получим необходимые выражения для производных. Когда правые части уравнений (2.2) или (2.4) включают выражения для воздействия и производную от воздействия следует использовать модифицированную запись уравнений (2.2) и (2.4):
где Апроксимация зависимости F(t) проводится описанными методами.
|

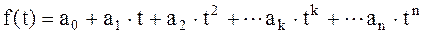 (2.6)
(2.6)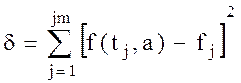 . (2.7)
. (2.7)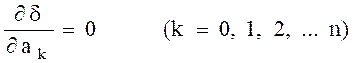 . (2.8)
. (2.8)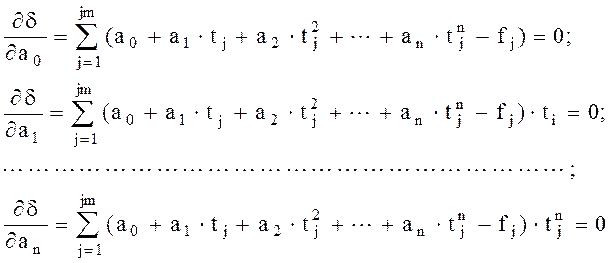 (2.9)
(2.9)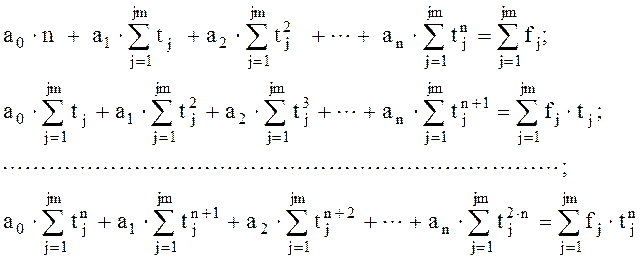 (2.10)
(2.10)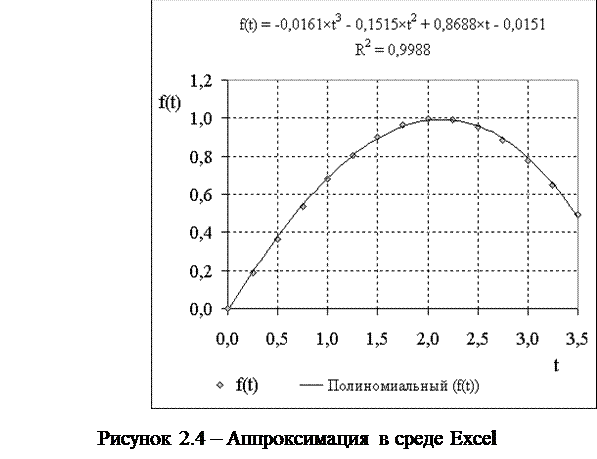 j
j
 , (2.12)
, (2.12)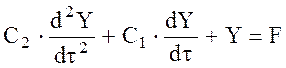 (2.13)
(2.13)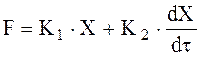 .
.


