Идентификация уравнения (1) в среде Excel
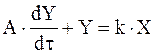 (1) (1)
где τ - время, X(τ) - воздействие, Y(τ) - реакция оъекта.
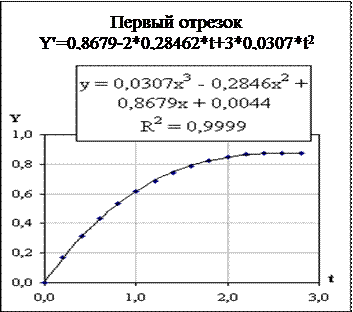
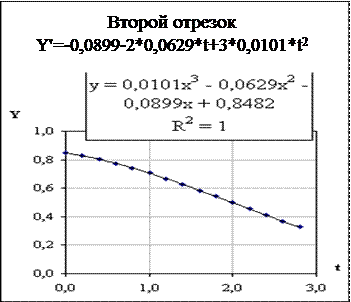
Используется аппроксимация на последовательных отрезках.
Выражение для суммы квадратов невязок по всем рассмотренным зонам имеет вид:
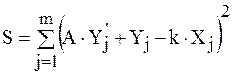 (4) (4)
где m – количество рассмотренных точек всей области определения функции (включая все выделенные интервалы),
j – индекс точки.
Необходимым условием минимума функции δ является равенство нулю ее частных производных:
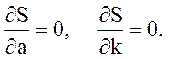 (5) (5)
 (6) (6)
Решив систему линейных алгебраических уравнений (6) получим значения A, k.
| m
| τ
| t
| X
| Y
| Y'
| (Y')2
| -X*Y'
| X2
| -Y*Y'
| X*Y
| |
|
| 0,0
| 1,842
| 0,000
| 0,868
| 0,7533
| -1,599
| 3,3930
|
|  0 0
| |
| 0,2
| 0,2
| 1,891
| 0,169
| 0,758
| 0,5742
| -1,433
| 3,5759
| -0,128
| 0,3196
| |
| 0,4
| 0,4
| 1,932
| 0,312
| 0,655
| 0,429
| -1,265
| 3,7326
| -0,204
| 0,6028
| |
| 0,6
| 0,6
| 1,964
| 0,432
| 0,56
| 0,3131
| -1,099
| 3,8573
| -0,242
| 0,8484
| |
| 0,8
| 0,8
| 1,985
| 0,533
| 0,471
| 0,2223
| -0,936
| 3,9402
| -0,251
| 1,058
| |
|
| 1,0
| 1,998
| 0,617
| 0,391
| 0,1527
| -0,781
| 3,9920
| -0,241
| 1,2328
| |
| 1,2
| 1,2
| 2,000
| 0,686
| 0,317
| 0,1008
| -0,635
| 4,0000
| -0,218
| 1,372
| |
| 1,4
| 1,4
| 1,992
| 0,743
| 0,252
| 0,0633
| -0,501
| 3,9681
| -0,187
| 1,4801
| |
| 1,6
| 1,6
| 1,974
| 0,788
| 0,193
| 0,0372
| -0,381
| 3,8967
| -0,152
| 1,5555
| |
| 1,8
| 1,8
| 1,946
| 0,823
| 0,142
| 0,0201
| -0,276
| 3,7869
| -0,117
| 1,6016
| |
|
| 2,0
| 1,909
| 0,848
| 0,098
| 0,0096
| -0,187
| 3,6443
| -0,083
| 1,6188
| |
| 2,2
| 2,2
| 1,863
| 0,866
| 0,061
| 0,0038
| -0,114
| 3,4708
| -0,053
| 1,6134
| |
| 2,4
| 2,4
| 1,809
| 0,875
| 0,032
| 0,001
| -0,058
| 3,2725
| -0,028
| 1,5829
| |
| 2,6
| 2,6
| 1,746
| 0,877
| 0,011
| 0,0001
| -0,018
| 3,0485
| -0,009
| 1,5312
| |
| 2,8
| 2,8
| 1,676
| 0,873
| -0,004
| 1E-05
| 0,006
| 2,8090
| 0,0033
| 1,4631
| |
|
| 3,0
| 1,599
| 0,863
| -0,011
| 0,0001
| 0,017
| 2,5568
| 0,0093
| 1,3799
| |
| 3,2
| 0,0
| 1,516
| 0,848
| -0,09
| 0,0081
| 0,136
| 2,2983
| 0,0762
|  1,2856 1,2856
| |
| 3,4
| 0,2
| 1,427
| 0,828
| -0,114
| 0,013
| 0,162
| 2,0363
| 0,0943
| 1,1816
| |
| 3,6
| 0,4
| 1,335
| 0,803
| -0,135
| 0,0183
| 0,181
| 1,7822
| 0,1087
| 1,072
| |
| 3,8
| 0,6
| 1,239
| 0,774
| -0,154
| 0,0239
| 0,191
| 1,5351
| 0,1196
| 0,959
| |
|
| 0,8
| 1,141
| 0,741
| -0,171
| 0,0293
| 0,195
| 1,3019
| 0,1268
| 0,8455
| |
| 4,2
| 1,0
| 1,042
| 0,706
| -0,185
| 0,0344
| 0,193
| 1,0858
| 0,1309
| 0,7357
| |
| 4,4
| 1,2
| 0,942
| 0,667
| -0,197
| 0,0389
| 0,186
| 0,8874
| 0,1316
| 0,6283
| |
| 4,6
| 1,4
| 0,842
| 0,627
| -0,207
| 0,0427
| 0,174
| 0,7090
| 0,1296
| 0,5279
| |
| 4,8
| 1,6
| 0,745
| 0,585
| -0,214
| 0,0456
| 0,159
| 0,5550
| 0,125
| 0,4358
| |
|
| 1,8
| 0,649
| 0,542
| -0,218
| 0,0476
| 0,142
| 0,4212
| 0,1182
| 0,3518
| |
| 5,2
| 2,0
| 0,558
| 0,498
| -0,22
| 0,0485
| 0,123
| 0,3114
| 0,1097
| 0,2779
| |
| 5,4
| 2,2
| 0,470
| 0,454
| -0,22
| 0,0484
| 0,103
| 0,2209
| 0,0999
| 0,2134
| |
| 5,6
| 2,4
| 0,388
| 0,411
| -0,217
| 0,0472
| 0,084
| 0,1505
| 0,0893
| 0,1595
| |
| 5,8
| 2,6
| 0,312
| 0,368
| -0,212
| 0,045
| 0,066
| 0,0973
| 0,0781
| 0,1148
| |
|
| 2,8
| 0,243
| 0,326
| -0,205
| 0,0419
| 0,05
| 0,0590
| 0,0667
| 0,0792
| |
| 6,2
| 3,0
| 0,182
| 0,286
| -0,195
| 0,0379
| 0,035
| 0,0331
| 0,0557
| 0,0521
| |
|
|
|
|
| Σ=
| 3,213
| -7,114
| 70,40
| -0,297
| 28,13
| | | | | | | | | | | | | | | | |

|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
| 3,213
| -7,11
|
|
|
| 
|
| |
|
|
|
|
|
| -7,11
| 70,40
|
|
| 28,13
|
|
| |
| 
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
| 0,401
| 0,040
|
| A=
|
| 
|
| |
|
|
|
|
|
| 0,040
| 0,018
|
| k=
| 0,494
|
|
| |
| Примечание: Следует помнить, что при представлении формулы линии тренда (как и при работе с диаграммами) X- имя аргумента, Y - имя функции.
|

Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|
Хронометражно-табличная методика определения суточного расхода энергии студента Цель: познакомиться с хронометражно-табличным методом определения суточного расхода энергии...
ОЧАГОВЫЕ ТЕНИ В ЛЕГКОМ Очаговыми легочными инфильтратами проявляют себя различные по этиологии заболевания, в основе которых лежит бронхо-нодулярный процесс, который при рентгенологическом исследовании дает очагового характера тень, размерами не более 1 см в диаметре...
Примеры решения типовых задач. Пример 1.Степень диссоциации уксусной кислоты в 0,1 М растворе равна 1,32∙10-2
Пример 1.Степень диссоциации уксусной кислоты в 0,1 М растворе равна 1,32∙10-2. Найдите константу диссоциации кислоты и значение рК.
Решение. Подставим данные задачи в уравнение закона разбавления
К = a2См/(1 –a) =...
|
Условия, необходимые для появления жизни История жизни и история Земли неотделимы друг от друга, так как именно в процессах развития нашей планеты как космического тела закладывались определенные физические и химические условия, необходимые для появления и развития жизни...
Метод архитекторов Этот метод является наиболее часто используемым и может применяться в трех модификациях: способ с двумя точками схода, способ с одной точкой схода, способ вертикальной плоскости и опущенного плана...
Примеры задач для самостоятельного решения. 1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P
1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P...
|
|

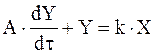 (1)
(1)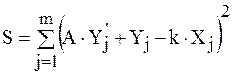 (4)
(4)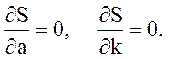 (5)
(5) (6)
(6) 0
0
 1,2856
1,2856







