Основы метода
Для решения задачи идентификации чаще всего выбирается метод наименьших квадратов с аппроксимацией зависимостей X=f(τ) и Y=f(τ) при котором: 1) проводится аппроксимация зависимостей X=f(τ) и Y=f(τ) на отрезках оси времени гладкими функциями (полиномы невысоких степеней); 2) для моментов времени путем дифференцирования аппроксимирующих функций определяются производные 3) значения функций и производных подставляются в идентифицируемое уравнение и определяется сумма квадратов невязок левой и правой частей уравнения для всех рассматриваемых моментов времени; 4) значения коэффициентов идентифицируемого дифференциального уравнения определяются путем минимизации суммы квадратов невязок левой и правой частей уравнения.
|

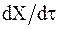 ,
, 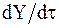 ,
, 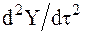 .
.


