Внутренняя норма доходности
Внутренняя норма доходности (ВНД); проверочный дисконт, обозначается IRR (internal rate of return) - норма дисконта, при которой уравновешивается текущая стоимость притоков денежных средств и текущая стоимость их оттоков, образовавшихся в результате реализации инвестиционного проекта. Если IRR для проекта больше требуемой инвестором отдачи, (минимальной нормы доходности), то проект принимают, если ниже - отклоняют. Экономический смысл этого показателя: можно принимать инвестиционное решение, уровень доходности которого не ниже цены источника средств для данного проекта. Чаще всего можно увидеть сопоставление со ставкой банковского процента, если проект финансируется за счет банковского кредита. Процедура расчета не очень сложна и определяется решением уравнения
NPVт = 0 или
При отсутствии финансового калькулятора применяют метод последовательных итераций. Если обозначить NPV =
IRR = r1 +
где r1 - значение нормы дисконтирования, при которой f(r1) > 0; r2 - значение нормы дисконтирования, при котором f(r2) < 0. Расчет дает достаточно достоверный результат, если r1 и r2 различаются не более чем один - два процентных пункта (в абсолютном выражении). Пример 4.14. Проект рассчитан на четыре года. Денежные потоки по годам: 0-й год (вложения средств) = первоначальные инвестиции в 10 млн р., 1-й год - доходы 3 млн р., 2-й - доходы 4 млн р., 3-й год - доходы 7 млн р. Определите IRR. Решение: При r = 0,10 %, NPV = 1,29 млн р.; при r = 20 %, NPV = - 0,67 млн р., тогда IRR = 10 % +1,29 (20 % - 10 %):(1,29 - (-0,67)) = 16,6 %. Уточним, при r = 16 %, NPV = 0,05, при r = 17 %, NPV = - 0,14, следовательно, уточненное решение IRR = 16 % + 0,05(17 % - 16 %)(0,05 - (-0,14)) = = 16,26 %. Обычно такие расчеты показывают в табл. 4.3. Таблица 4.3 Исходные данные для расчета IRR
Графически можно показать IRR на рис. 4.10.
Проблемы возникают при оценке IRR, если поток платежей предусматривает капитальные вложения в будущем, например, на ремонт и модернизацию дорог, рекультивацию земель и т. п.; тогда проект может иметь или несколько значений IRR, или ни одного решения. В первом случает выбирают наименьшее значение IRR, во втором - используют иные методы или критерии для оценки проектов.
IRR r IRR1 IRR2 IRR3
Рис. 4.10. Зависимость NPV от ставки сравнения
Ограничения применения метода IRR связаны, во-первых с тем, что при его использовании не учитывается масштаб инвестирования, поэтому может быть отклонен проект, имеющий большую величину NPV, как это показано на примере (табл. 4.4).
Таблица 4.4
Вторая проблема использования метода IRR связана с тем, что он предполагает реинвестирование средств, получаемых от реализации проекта по ставке, равной IRR при данном оставшемся сроке реализации проекта, а это, особенно при высоких значениях IRR, маловероятно. Наиболее часто допускается ошибка при выборе альтернативных проектов при использовании IRR: считается, что всегда лучше проект с наибольшим значением IRR. Это далеко не всегда так, что становится очевидным из примера 4.15. Пример 4.15. Пусть имеются два стандартных альтернативных проекта с первоначальными инвестициями С01 и С02 и ежегодным эффектом П1 и П2, период действия - Т лет. Как видно из рис. 4.11, IRR1 > IRR2, но это не обязательно означает, что первый проект лучше.
(ТП2-С02)
ЕF IRR1
- С01
Рис. 4.11
Первый проект лучше только в том случае, когда фактически стоимость капитала Е > ЕF. ЕF - точка Фишера, определяемая условиями равенства по проектам значений NPV. Если Е < ЕF, то NPV1 < NPV2 и лучше второй вариант с меньшим значением IRR.
|

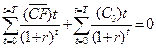 . (4.14)
. (4.14)
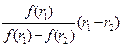 , (4.15)
, (4.15)
 а) NPV б) NPV
а) NPV б) NPV

 NPV
NPV
 (ТП1-С01)
(ТП1-С01) 0 IRR2
0 IRR2
 - C02
- C02


