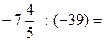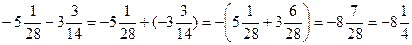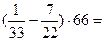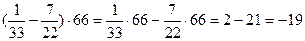Актуализация.
- На доске записаны задания. Работа идет устно со всем классом. № 1. Какие из предложенных чисел являются: 1) натуральными; 2) целыми;3) рациональными? а) Ответ: 1) г; 2) б, г, е; 3) все.
- Итак, вы на уроках математики так же, как это происходило и в истории математики, постепенно пришли от понятия натурального числа к понятию рационального числа. И теперь вы умеете выполнять действия с числами различных видов. Вспомним, какие это действия. № 2. Вычислите: а) б) - - Сформулируйте правило сложения чисел с разными знаками. («Чтобы сложить два числа с разными знаками надо: 1) сравнить модули этих чисел; 2) из большего модуля вычесть меньший; 3) поставить перед полученной разностью знак того слагаемого, модуль которого больше»)
б) - Сформулируйте правило сложения двух отрицательных чисел. («Чтобы сложить два отрицательных числа надо: 1) сложить их модули; 2) поставить пред полученной суммой знак -»)
в) - Сформулируйте правило умножения чисел с разными знаками. («Чтобы перемножить два числа с разными знаками надо: 1) перемножить модули этих чисел; 2) поставить перед полученным произведением знак –») г) - Сформулируйте правило деления двух отрицательных чисел. («Чтобы найти частное от деления двух отрицательных чисел надо: 1) разделить модули этих чисел; 2) поставить пред полученным частным знак +») № 3. Вычислите наиболее рациональным способом: а) б) (Учащиеся вычисляют и называют используемые при вычислении свойства, учитель записывает в схематическом виде на доске их, а учащиеся в тетради); Ответы: - Какое свойство сложения вы использовали? (Сочетательное свойство (на доску записывается: a+(b+c)=(a+b)+c)) б) - Какой закон вы использовали? (Распределительный закон умножения относительно вычитания (на доске появляется запись: а(b-c)=ab-ас))
|

 б)
б)  в)
в)  г)
г)  д)
д) 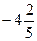 е) 0
е) 0 в)
в) 
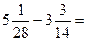 г)
г)