ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Количественно эффект Джоуля-Томсона характеризуется дифференциальным коэффициентом Джоуля-Томсона:
Величина m может быть как положительной, так и отрицательной. В первом случае газ при расширении охлаждается ( Для того чтобы выяснить, почему эффект Джоуля - Томсона проявляется только в отношении реальных газов, рассмотрим процесс расширения газа в пустоту подробнее, для чего вновь обратимся к выше упомянутой модели. Очевидно, что рассмотренный процесс сопровождается совершением работы газа против внешних сил. Если скорость движения левого поршня такова, что давление газа слева от пористой перегородки остается постоянным, то и давление газа справа от перегородки окажется постоянным на всем протяжении эксперимента. Изменяться будут только объемы газа: в левой области от
Общая работа газа равна:
Так как рассмотренный процесс протекает адиабатически, то согласно первому началу термодинамики, совершенная газом работа полностью расходуется только на изменение внутренней энергии газа: Тогда:
Функция состояния
называется энтальпией газа, которая согласно (2), остается постоянной по обе стороны от перегородки:
Поскольку для идеального газа все три величины, входящие в (4), зависят только от температуры, то и энтальпия идеального газа является функцией только температуры. Тогда постоянство энтальпии означает и постоянство температуры идеального газа. Иначе дело обстоит с реальным газом. Его внутренняя энергия, помимо температуры, зависит еще и от объема газа. Поэтому для реального газа постоянство энтальпии не означает постоянства температуры газа. Перепишем уравнение (4) в виде:
Т. к.
то
Учитывая, что зависимость изменения энтропии
перепишем уравнение (5) в виде:
Это уравнение позволяет определить величину дифференциального коэффициента Джоуля-Томсона:
где Согласно (6) при Получить численное значение коэффициента Джоуля-Томсона можно, вычислив производную
в виде
и продифференцируем это уравнение по T при постоянном давлении p:
Подставляя вместо p его значение из уравнения Ван-дер-Ваальса
получим:
Тогда окончательно имеем:
При не очень высоком давлении (порядка 100-200 атм), когда
Из формулы (8) следует, что коэффициент Джоуля-Томсона положителен при
Сопоставляя это выражение с выражением для критической температуры
получаем соотношение между температурой инверсии и критической температурой:
|

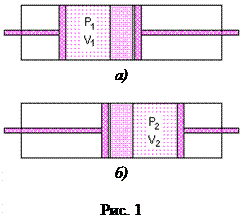 Эффект Джоуля - Томсона заключается в зависимости температуры реального газа от его объема и проявляется при адиабатном расширении газа в пустоту. Рассмотрим проявление этого эффекта на примере следующей модели. Пусть дан цилиндр с теплоизолирующими стенками (рис. 1). В средней части цилиндра находится пористая перегородка, с каждой стороны перегородки - по поршню. Пусть правый поршень придвинут вплотную к перегородке, а левый отстоит от нее на некотором расстоянии (рис. 1. а). Обозначим объем и давление газа, заключенного между перегородкой и левым поршнем, через
Эффект Джоуля - Томсона заключается в зависимости температуры реального газа от его объема и проявляется при адиабатном расширении газа в пустоту. Рассмотрим проявление этого эффекта на примере следующей модели. Пусть дан цилиндр с теплоизолирующими стенками (рис. 1). В средней части цилиндра находится пористая перегородка, с каждой стороны перегородки - по поршню. Пусть правый поршень придвинут вплотную к перегородке, а левый отстоит от нее на некотором расстоянии (рис. 1. а). Обозначим объем и давление газа, заключенного между перегородкой и левым поршнем, через  и
и  . Очевидно, что те же величины по правую сторону от перегородки окажутся равными нулю:
. Очевидно, что те же величины по правую сторону от перегородки окажутся равными нулю:  ;
; 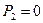 . Начнем медленно перемещать левый поршень в сторону перегородки, что приведет к росту давления
. Начнем медленно перемещать левый поршень в сторону перегородки, что приведет к росту давления  и давление
и давление  газа справа от перегородки начнут возрастать до тех пор, пока весь газ из левой области цилиндра не перейдет в правую его область (рис. 1. б.). Если процесс протекал адиабатно, то, как показывает опыт, наблюдается изменение температуры дросселировавшего газа.
газа справа от перегородки начнут возрастать до тех пор, пока весь газ из левой области цилиндра не перейдет в правую его область (рис. 1. б.). Если процесс протекал адиабатно, то, как показывает опыт, наблюдается изменение температуры дросселировавшего газа. . (1)
. (1) - положительный эффект Джоуля-Томсона), а во втором - нагревается (
- положительный эффект Джоуля-Томсона), а во втором - нагревается (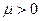 - отрицательный эффект Джоуля-Томсона). Следует так же заметить, что коэффициент Джоуля-Томсона способен менять свой знак при переходе газа из одной области температур в другую. Температура
- отрицательный эффект Джоуля-Томсона). Следует так же заметить, что коэффициент Джоуля-Томсона способен менять свой знак при переходе газа из одной области температур в другую. Температура  , при которой коэффициент Джоуля - Томсона для данного газа меняет свой знак, называется температурой инверсии.
, при которой коэффициент Джоуля - Томсона для данного газа меняет свой знак, называется температурой инверсии.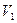 до 0, а в правой - от 0 до
до 0, а в правой - от 0 до 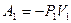 и
и 
 .
.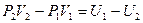 или
или 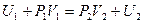 . (2)
. (2)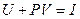 (3)
(3)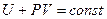 или
или 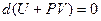 . (4)
. (4) .
.
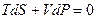 (5)
(5)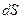 от изменения температуры
от изменения температуры 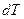 и от изменения давления
и от изменения давления 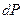 имеет вид
имеет вид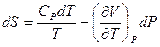 ,
,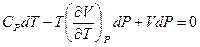 .
.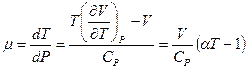 , (6)
, (6) - термический коэффициент расширения газа.
- термический коэффициент расширения газа.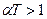 коэффициент
коэффициент 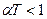 имеем
имеем 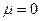 и, следовательно,
и, следовательно,  .
.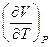 , входящую в уравнение (6). Для этого перепишем уравнение Ван-дер-Ваальса
, входящую в уравнение (6). Для этого перепишем уравнение Ван-дер-Ваальса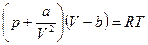
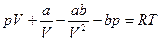
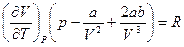
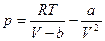 ,
,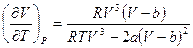 .
.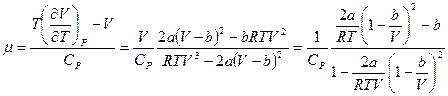 . (7)
. (7)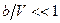 и
и  , уравнение (7) можно переписать в виде:
, уравнение (7) можно переписать в виде: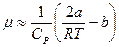 . (8)
. (8)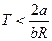 и отрицателен в противном случае. Таким образом, температура инверсии может быть определена равенством:
и отрицателен в противном случае. Таким образом, температура инверсии может быть определена равенством: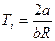 . (9)
. (9)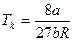 ,
,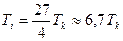 .
.


