Элементарная теория классического эффекта Холла (для носителей заряда одного типа)
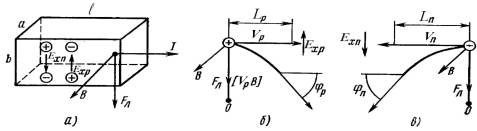
Сущность классического эффекта Холла заключается в возникновении ЭДС, называемой ЭДС Холла, в направлении, перпендикулярном направлению тока, протекающего через образец, и направлению действующего на образец магнитного поля. Впервые появление поперечной (холловской) разности потенциалов в образце, находящемся в таких условиях, было зарегистрировано Э. Холлом в 1879 году на тонких пластинах золота. Появление холловской разности потенциалов связано с действием силы Лоренца на движущиеся в кристалле заряды. Для количественного рассмотрения предположим, что образец полупроводника в виде прямоугольного параллелепипеда (рис. 2.1, а) имеет ширину а, толщину b и длину l, а ток протекает слева направо. В случае, если ток создается дырками, то скорость дрейфа V p имеет то же направление, что и ток I (рис. 2.1, а, б). Если же носителями тока являются электроны, то V n направлена в противоположную сторону (рис. 2.1, а, в).
Поместим полупроводник во внешнее магнитное поле, чтобы индукция В была направлена перпендикулярно току (к нам). При наличии внешнего магнитного поля на движущиеся носители тока действует сила Лоренца, которая перпендикулярна скорости их движения V и индукции магнитного поля B:
Для дырок векторное произведение и сила Лоренца будут направлены вниз, тогда как для электронов, заряд которых отрицателен, векторное произведение направлено вверх, а сила Лоренца – вниз (правило левой руки). Следовательно, как дырки (в полупроводнике p -типа), так и электроны (в полупроводнике n -типа) будут отклоняться магнитным полем на нижнюю грань, а верхняя грань будет обедняться в первом случае дырками, во втором – электронами. Таким образом, в полупроводнике р- типа нижняя грань заряжается положительно, а верхняя грань – отрицательно. В результате возникает поперечное электрическое поле, называемое холловским полем, с напряженностью Еx, которое направленно снизу вверх. В полупроводнике n –типа нижняя грань (при том же направлении тока) заряжается отрицательно, верхняя – положительно и холловское поле направлено сверху вниз. Если в переносе электрического тока участвуют и дырки и электроны (случай смешанной проводимости), то картина значительно усложняется. Этот случай рассмотрен в Приложении А. Положения дырки и электрона, отклоненных магнитным полем при дрейфовом перемещении на протяжении длины свободного пробега Lp и Ln изображены на рис. 2.1. При этом предполагается, что холловское поле еще отсутствует. Углы φn и φp называют углами Холла. Если изобразить векторы плотности тока дырок и электронов, то, учитывая направления поворотов φn и φp, имеем, что плотности тока jp и jn поворачиваются в противоположные стороны (рис. 2.2 а, б). Здесь предполагается, что либо холловское поле еще не действует, либо имеется неограниченный по направлению b образец (последнее можно моделировать с помощью образца в виде диска).
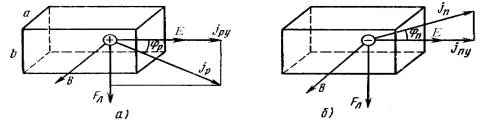
В обычных условиях для ограниченного образца полупроводника накопление зарядов, отклоненных магнитным полем, происходит до тех пор, пока не уравновесятся силы, действующие на электрон (то есть сила, связанная с возникающим холловским полем не нейтрализует силу Лоренца). После достижения указанного динамического равновесия можно считать, что при наличии одного типа носителей заряда плотность тока jp и jn не отклоняется магнитным полем. Следовательно, при дальнейшем длительном пребывании полупроводника с током в поперечном магнитном поле устанавливается определенная поперечная разность потенциалов, которая при разомкнутой цепи и есть ЭДС Холла. Полная напряженность поля En является векторной суммой E и Exn составляет с E угол Холла φ; (рис. 2.3).
Итак, при одном типе носителей заряда условием, определяющим холловское поле, является равенство абсолютных значений силы Лоренца и силы возникающего холловского поля:
или
Равенство (2.3) не может выполняться одновременно для всех электронов (дырок), имеющих различные по величине и направлению скорости. В действительности стационарное состояние наступает не тогда, когда сила Лоренца уравновешивает силу электрического поля для каждого электрона (это вообще не может быть), а когда ток, создаваемый холловским полем, компенсирует ток на боковую грань, создаваемый магнитным полем. Поэтому в выражении (2.3) стоит средняя скорость Умножая обе части (2.3) на концентрацию электронов n, получим для полупроводника n –типа
Поскольку произведение neVср равно плотности тока, то есть:
где а·b=S – площадь поперечного сечения образца, показанного на рис. 2.1, то на основании (2.4) и (2.5) получаем
Разность потенциалов
Более точные расчеты, выполненные с учетом статистического распределения носителей заряда по скоростям в невырожденных полупроводниках, показывают, что
где А – постоянная величина, так называемый холл–фактор. Его значение определяется механизмами рассеяния. Для полупроводниковых материалов основными механизмами рассеяния носителей тока являются рассеяние на тепловых колебаниях решетки и на ионах примесей. При рассеянии электронов на акустических колебаниях решётки, что имеет место в классических полупроводниковых материалах (например, в Si, Ge, InSb) при относительно высоких температурах (включая комнатную),
Для полупроводника n -типа формулу (2.8) можно переписать в виде
где е – заряд электрона. Коэффициент пропорциональности
называют постоянной Холла или коэффициентом Холла. Для полупроводника р –типа коэффициент Холла
Соотношения (2.8), (2.10) и (2.11) играют чрезвычайно важную роль в физике полупроводников. Они показывают, что концентрация носителей заряда, их знак могут быть найдены экспериментально. Для этого необходимо в образце с известными геометрическими размерами измерить холловскую разность потенциалов и определить коэффициент Холла:
Зная коэффициент Холла и удельную электрическую проводимость
Следует иметь ввиду, что холловская подвижность совпадает с дрейфовой только при А =1. Входящую в выражение (2.13) величину
где l, a, b – геометрические параметры образца.
Необходимо отметить, что при выводе выражения для коэффициента Холла и холловской подвижности использовались формулы (2.5) и (2.12), которые справедливы только в случае, когда магнитное поле отсутствует либо оно мало. Условие слабого магнитного поля можно записать в виде
|

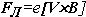
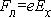
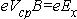
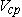 дрейфа.
дрейфа.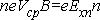
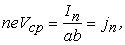
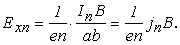
 = Exnb будет иметь вид:
= Exnb будет иметь вид: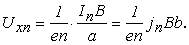
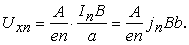
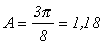
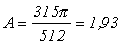
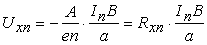
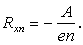
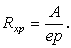
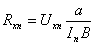
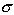 материала, можно рассчитать холловскую подвижность
материала, можно рассчитать холловскую подвижность 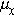 . Действительно, домножив обе части уравнения типа (2.10) на
. Действительно, домножив обе части уравнения типа (2.10) на 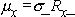
 (см. ниже), или же, если известно сопротивление образца Rобр, рассчитать, воспользовавшись формулой:
(см. ниже), или же, если известно сопротивление образца Rобр, рассчитать, воспользовавшись формулой: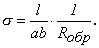
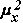
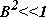 . Как правило, это условие выполняется при измерении эффекта Холла.
. Как правило, это условие выполняется при измерении эффекта Холла.


