ПРИЛОЖЕНИЕ А. Рассмотрим полупроводник со смешанной электропроводностью, в котором нельзя пренебрегать ни электронами
Теория эффекта Холла для полупроводника со смешанной электропроводностью. Рассмотрим полупроводник со смешанной электропроводностью, в котором нельзя пренебрегать ни электронами, ни дырками. Как указывалось, векторы плотности токов
Полная плотность тока j является векторной суммой плотностей токов
Выберем оси координат так, чтобы ось x была направлена по полю или против поля Холла, ось у – по внешнему полю E, ось z – по магнитному полю В. Тогда для тангенса угла j (малого) имеем
где
Здесь положили
Ввиду малости углов jp и jn синусы заменены на углы. Последние можно выразить из отношений, очевидных из рис. 1п. Этот рисунок соответствует динамическому равновесию, и поле Холла достигает установившегося значения. Имеем:
Причем E можно выразить следующим образом:
Это использовано в соотношении (1п.3).
Согласно (2.9):
Следовательно, имеем
Подставляя (1п.11) и (1п.12) в (1п.4), получаем
Еcли подставим (1п.13) и (1п.3) в выражение (1п.2), то
Кроме того, по формуле (1п.11)
Аналогичным образом для угла j можно записать
где σ=e(pµp+nµn).
Сравнивая (1п.14) и (1п.16), имеем
Таким образом, получено общее выражение для коэффициента Холла. Оно справедливо, например, для случая, когда электропроводность возникает в нескольких зонах одновременно при участии нескольких сортов носителей. Обычно это электроны зоны проводимости и дырки валентной зоны в области собственной проводимости в сильно компенсированных материалах или так называемых полуизоляторах, либо возбуждённые, например светом, неравновесные носители. Соотношения (1п.10) и (1п.11) вытекают из него как частные случаи, если положить р=0 или n=0. Из выражения (1п.17) видно, что понятие "вклада" носителей разного типа в эффект Холла существенно отлично от их вклада в электропроводность. Во-первых, вклад разностный, а во-вторых, вклады электронов и дырок усиливаются произведениями концентраций на квадраты подвижностей. В области собственной проводимости согласно (1п.17)
Поскольку обычно mn> mp, то Rxi является величиной отрицательной. Как видно из соотношений (1п.11) и (1п.12), углы Холла дырок и электронов пропорциональны произведению подвижностей на индукцию магнитного поля. Кроме дрейфовых подвижностей, вводят понятие холловских подвижностей, которые определяют в виде
Холловские подвижности при А=1 совпадают с дрейфовыми. Ранее использовались приближенные выражения в предположении малости углов jp, jn, j. Соответственно магнитные поля, для которых указанные углы малы, называют слабыми. Критерии слабого магнитного поля выражаются неравенствами:
где
|

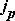 и
и  отклоняются в разные стороны, поэтому для смешанного полупроводника необходимо изображать диаграмму токов. На рис. 1п. показана эта диаграмма в предположении, что холловское поле еще не действует.
отклоняются в разные стороны, поэтому для смешанного полупроводника необходимо изображать диаграмму токов. На рис. 1п. показана эта диаграмма в предположении, что холловское поле еще не действует.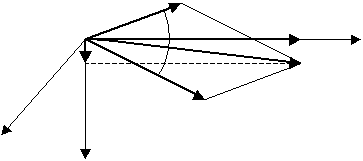
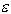 , создающего дрейф носителей заряда. Следовательно,
, создающего дрейф носителей заряда. Следовательно,
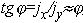
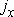 и
и 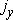 – составляющие вектора полного тока по осям х и у (имеются в виду абсолютные значения всех величин). В соответствии с рис. 1п.
– составляющие вектора полного тока по осям х и у (имеются в виду абсолютные значения всех величин). В соответствии с рис. 1п.
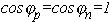 , считая углы
, считая углы 
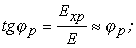

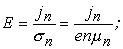

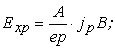
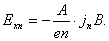
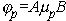
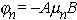

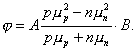
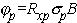

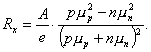

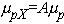

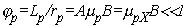

 и
и 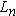 – длины свободного пробега дырок и электронов;
– длины свободного пробега дырок и электронов;  и
и 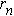 – радиусы дуг окружностей, по которым закручиваются дырки и электроны под действием силы Лоренца. В частности, например, для германия при
– радиусы дуг окружностей, по которым закручиваются дырки и электроны под действием силы Лоренца. В частности, например, для германия при  и В= 1 Тл неравенство (1п.22) выполняется. Поскольку подвижность дырок меньше подвижности электронов, то (1п.21) также выполняется. Причем индукция 1 Тл является "слабой" условно только с точки зрения выполнения указанных неравенств. В сильных полях, которые определяются неравенствами с противоположным знаком, коэффициент А=1. Для металлов и вырожденных полупроводников, независимо от величины В, имеем А=1.
и В= 1 Тл неравенство (1п.22) выполняется. Поскольку подвижность дырок меньше подвижности электронов, то (1п.21) также выполняется. Причем индукция 1 Тл является "слабой" условно только с точки зрения выполнения указанных неравенств. В сильных полях, которые определяются неравенствами с противоположным знаком, коэффициент А=1. Для металлов и вырожденных полупроводников, независимо от величины В, имеем А=1.


