Математическое описание
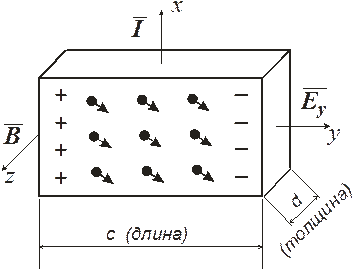
Эффект Холла Сущность физического эффекта: Если поместить полупроводник, через который протекает электрический или тепловой поток в магнитное поле, то в нём возникают гальваномагнитные явления. Гальваномагнитные явления возникают в полупроводниках при одновременном воздействии электрического и магнитного полей. К гальваномагнитным явлениям относятся и эффект Холла. Суть эффекта Холла заключается в следующем. При пропускании электрического тока вдоль полупроводника, помещённого в магнитное поле, силовые линии которого направлены перпендикулярно направлению электрического тока, возникает поперечная разность потенциалов, называемая ЭДС Холла. Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов при помещении проводника с постоянным током в магнитное поле. Математическое описание Рассмотрим полупроводник, например, n –типа электропроводности, имеющий форму параллелепипеда. Пусть электрический ток движется вдоль оси OX. Перпендикулярно направлению электрического тока вдоль оси OZ направлено магнитное поле. Под действием силы, действующей со стороны магнитного поля, электроны будут отклоняться на боковую грань полупроводника. Таким образом, на одной из граней полупроводника будут накапливаться электроны, в результате чего она зарядится отрицательно, а на противоположной грани возникает нескомпенсированный положительный заряд. Это приведёт к образованию поперечного электрического поля напряжённостью На заряд q, который движется в магнитном поле с индукцией
Рис. 1. Возникновение эффекта Холла Под действием силы Лоренца движущиеся электроны отклоняются на одну из боковых граней полупроводника. Процесс накопления носителей заряда продолжается до тех пор, пока сила Лоренца не уравновесится силой, действующей со стороны поперечного электрического поля. Сила
При исследовании электрофизических свойств полупроводников методом эффекта Холла измеряют не величину напряжённости поперечного электрического поля
Скорость электронов
Отсюда получим
где n – концентрация свободных электронов; с и d – поперечные размеры полупроводника. Подставим уравнения (2) и (3) в формулу (1), получим
Умножим правую и левую части этого уравнения на величину с:
Введём обозначения Отсюда для Rx имеем
Здесь Rx – постоянная Холла. Она связывает ЭДС Холла, силу тока и индукцию магнитного поля B. Зная величину постоянной Холла Rx, можно определить концентрацию свободных носителей заряда:
где p – концентрация дырок. Знак постоянной Холла совпадает со знаком носителей заряда. Следовательно, по величине Rx можно судить о типе электропроводности. Например, для электронного типа проводимость Rx <0, для дырочного типа электропроводности Rx >0. При выводе уравнения для ЭДС Холла сделан ряд допущений, связанных с тем, что полная скорость электронов принимается раной дрейфовой скорости, т.е. не учитывается скорость хаотического теплового движение электронов и их распределение по скоростям.
|

 , направленного вдоль оси OY (рис. 1). Если электрический ток переносится дырками, то поперечное электрическое поле будет противоположно направлению полю Холла для полупроводника n -типа электропроводности.
, направленного вдоль оси OY (рис. 1). Если электрический ток переносится дырками, то поперечное электрическое поле будет противоположно направлению полю Холла для полупроводника n -типа электропроводности. , действует сила Лоренца
, действует сила Лоренца  , равная
, равная  , где
, где  – скорость движения носителей заряда, направленных вдоль оси OX. Так как угол между векторами
– скорость движения носителей заряда, направленных вдоль оси OX. Так как угол между векторами 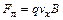 .
.
 , действующая со стороны электрического поля на заряд q, равна
, действующая со стороны электрического поля на заряд q, равна  . Она направлена в сторону, противоположную направлению силы Лоренца. В состоянии стационарного равновесия сила Лоренца равна силе, действующей со стороны поперечного электрического поля,
. Она направлена в сторону, противоположную направлению силы Лоренца. В состоянии стационарного равновесия сила Лоренца равна силе, действующей со стороны поперечного электрического поля, 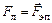 , т.е.
, т.е. 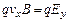 . Поделив правую и левую части этого уравнения на величину заряда электрона (q), получим:
. Поделив правую и левую части этого уравнения на величину заряда электрона (q), получим: (1)
(1)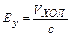 . (2)
. (2) выразим через величину силы тока I:
выразим через величину силы тока I: ,
, , (3)
, (3) .
. . (4)
. (4)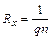 . С учётом такого обозначения формула (4) запишется в виде
. С учётом такого обозначения формула (4) запишется в виде 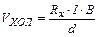 .
.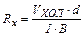 . (5)
. (5)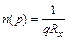 , (6)
, (6)


