1. Задание 4 № 27543. 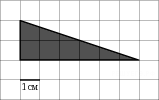 На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
2. Задание 4 № 27544. 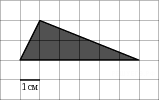 На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
3. Задание 4 № 27545.  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
4. Задание 4 № 27546.  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
5. Задание 4 № 27547.  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
6. Задание 4 № 27548. 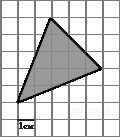 На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
7. Задание 4 № 27549.  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
8. Задание 4 № 27563.  Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (9;9).
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (9;9).
9. Задание 4 № 27564. 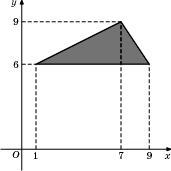 Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).
10. Задание 4 № 27565.  Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (10;9).
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (10;9).
11. Задание 4 № 27566.  Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;7), (7;10).
Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;7), (7;10).
12. Задание 4 № 27587.  Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8.
Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8.
13. Задание 4 № 27588.  Площадь прямоугольного треугольника равна 16. Один из его катетов равен 4. Найдите другой катет.
Площадь прямоугольного треугольника равна 16. Один из его катетов равен 4. Найдите другой катет.
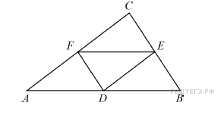
14. Задание 4 № 27592.  Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.
Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.
15. Задание 4 № 27617.  Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
16. Задание 4 № 27618.  Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.
Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.
17. Задание 4 № 27626.  Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.
Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.
18. Задание 4 № 27704. Найдите площадь треугольника, вершины которого имеют координаты (2; 2), (8; 10), (8; 8).
19. Задание 4 № 27743.  В треугольнике
В треугольнике 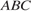 угол
угол 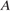 равен
равен  , внешний угол при вершине
, внешний угол при вершине  равен
равен  . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
20. Задание 4 № 27744.  В треугольнике
В треугольнике 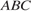 угол
угол 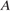 равен
равен 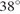 ,
,  . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
21. Задание 4 № 27745.  В треугольнике
В треугольнике 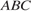 угол
угол  равен
равен 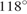 ,
,  . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
22. Задание 4 № 27746. 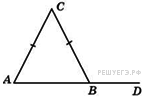 В треугольнике
В треугольнике 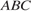
 , угол
, угол  равен
равен  . Найдите внешний угол
. Найдите внешний угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
23. Задание 4 № 27747.  В треугольнике
В треугольнике 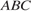
 . Внешний угол при вершине
. Внешний угол при вершине  равен
равен 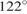 . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
24. Задание 4 № 27748.  В треугольнике
В треугольнике 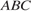
 . Внешний угол при вершине
. Внешний угол при вершине  равен
равен 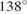 . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
25. Задание 4 № 27750.  Один из углов равнобедренного треугольника равен
Один из углов равнобедренного треугольника равен  . Найдите один из других его углов. Ответ дайте в градусах.
. Найдите один из других его углов. Ответ дайте в градусах.
26. Задание 4 № 27757. 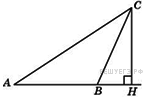 В треугольнике
В треугольнике 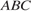 угол
угол 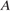 равен
равен  ,
, 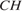 – высота, угол
– высота, угол  равен
равен 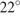 . Найдите угол
. Найдите угол 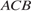 . Ответ дайте в градусах.
. Ответ дайте в градусах.
27. Задание 4 № 27758.  В треугольнике
В треугольнике 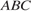
 – биссектриса, угол
– биссектриса, угол  равен
равен  , угол
, угол  равен
равен  . Найдите угол
. Найдите угол 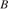 . Ответ дайте в градусах.
. Ответ дайте в градусах.
28. Задание 4 № 27759.  В треугольнике
В треугольнике 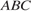
 – биссектриса, угол
– биссектриса, угол  равен
равен  , угол
, угол  равен
равен 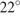 . Найдите угол
. Найдите угол 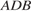 . Ответ дайте в градусах.
. Ответ дайте в градусах.
29. Задание 4 № 27760. 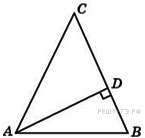 В треугольнике
В треугольнике 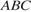
 ,
,  – высота, угол
– высота, угол 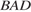 равен
равен 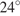 . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
30. Задание 4 № 27761. 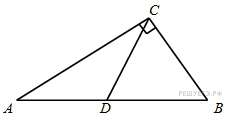 В треугольнике
В треугольнике 
 – медиана, угол
– медиана, угол  равен 90°, угол
равен 90°, угол  равен
равен  . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
31. Задание 4 № 27762. 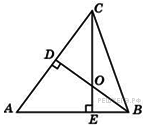 В треугольнике
В треугольнике 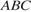 угол
угол 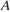 равен
равен  , а углы
, а углы  и
и  – острые.
– острые. 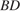 и
и  – высоты, пересекающиеся в точке
– высоты, пересекающиеся в точке 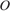 . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
32. Задание 4 № 27763.  Два угла треугольника равны
Два угла треугольника равны  и
и  . Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
33. Задание 4 № 27764.  В треугольнике
В треугольнике 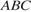 угол
угол  равен
равен  ,
,  и
и 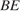 – биссектрисы, пересекающиеся в точке
– биссектрисы, пересекающиеся в точке 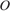 . Найдите угол
. Найдите угол 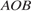 . Ответ дайте в градусах.
. Ответ дайте в градусах.
34. Задание 4 № 27765.  Острый угол прямоугольного треугольника равен
Острый угол прямоугольного треугольника равен 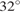 . Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
35. Задание 4 № 27766. 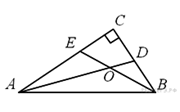 Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
36. Задание 4 № 27767. 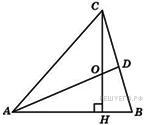 В треугольнике
В треугольнике 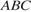
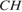 – высота,
– высота,  – биссектриса,
– биссектриса, 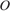 – точка пересечения
– точка пересечения 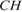 и
и  угол
угол  равен
равен 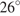 . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
37. Задание 4 № 27768. 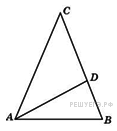 В треугольнике
В треугольнике  проведена биссектриса
проведена биссектриса  и
и  . Найдите меньший угол треугольника
. Найдите меньший угол треугольника  . Ответ дайте в градусах.
. Ответ дайте в градусах.
38. Задание 4 № 27769.  В треугольнике
В треугольнике  угол
угол 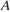 равен
равен  , угол
, угол  равен
равен 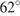 . На продолжении стороны
. На продолжении стороны  отложен отрезок
отложен отрезок  . Найдите угол
. Найдите угол 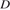 треугольника
треугольника  . Ответ дайте в градусах.
. Ответ дайте в градусах.
39. Задание 4 № 27770.  Острые углы прямоугольного треугольника равны
Острые углы прямоугольного треугольника равны  и
и  . Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
40. Задание 4 № 27771.  В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен
В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 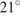 . Найдите меньший угол данного треугольника. Ответ дайте в градусах.
. Найдите меньший угол данного треугольника. Ответ дайте в градусах.
41. Задание 4 № 27772.  Острые углы прямоугольного треугольника равны
Острые углы прямоугольного треугольника равны  и
и 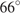 . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
42. Задание 4 № 27773.  В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
43. Задание 4 № 27774. 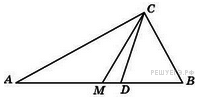 Острые углы прямоугольного треугольника равны
Острые углы прямоугольного треугольника равны  и
и 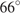 . Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
44. Задание 4 № 27775.  Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен
Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен  . Найдите меньший угол этого треугольника. Ответ дайте в градусах.
. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
45. Задание 4 № 27776.  В треугольнике
В треугольнике 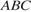 угол
угол  равен
равен  , угол
, угол  равен
равен 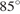 ,
, 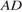 — биссектриса,
— биссектриса, 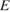 — такая точка на
— такая точка на  , что
, что  . Найдите угол
. Найдите угол 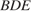 . Ответ дайте в градусах.
. Ответ дайте в градусах.
46. Задание 4 № 27777.  В треугольнике
В треугольнике 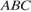 угол
угол  равен
равен  , угол
, угол  равен
равен  ,
, 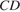 – биссектриса внешнего угла при вершине
– биссектриса внешнего угла при вершине  , причем точка
, причем точка  лежит на прямой
лежит на прямой  . На продолжении стороны
. На продолжении стороны  за точку
за точку  выбрана такая точка
выбрана такая точка 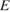 , что
, что  . Найдите угол
. Найдите угол  . Ответ дайте в градусах
. Ответ дайте в градусах
47. Задание 4 № 27778. 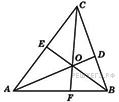 В треугольнике
В треугольнике 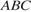 угол
угол  равен
равен  , угол
, угол  равен
равен 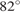 .
. 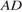 ,
, 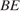 и
и 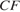 – биссектрисы, пересекающиеся в точке
– биссектрисы, пересекающиеся в точке 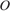 . Найдите угол
. Найдите угол 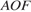 . Ответ дайте в градусах.
. Ответ дайте в градусах.
48. Задание 4 № 27779.  В треугольнике
В треугольнике 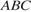 угол
угол  равен
равен  , угол
, угол  равен
равен 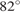 .
. 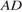 ,
, 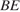 и
и 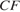 – высоты, пересекающиеся в точке
– высоты, пересекающиеся в точке 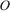 . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
49. Задание 4 № 27780.  На рисунке угол 1 равен
На рисунке угол 1 равен 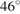 , угол 2 равен
, угол 2 равен  , угол 3 равен
, угол 3 равен  . Найдите угол 4. Ответ дайте в градусах.
. Найдите угол 4. Ответ дайте в градусах.
50. Задание 4 № 27794.  В треугольнике
В треугольнике 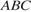
 ,
,  , высота
, высота 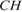 равна
равна 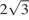 . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
51. Задание 4 № 27796.  В треугольнике
В треугольнике 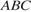
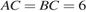 , высота
, высота  равна 3. Найдите угол
равна 3. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
52. Задание 4 № 244982.  Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
53. Задание 4 № 317337. В треугольнике ABC отрезок DE — средняя линия. Площадь треугольника CDE равна 38. Найдите площадь треугольника ABC.
54. Задание 4 № 319058. Площадь треугольника ABC равна 12. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABDE.
55. Задание 4 № 500905. 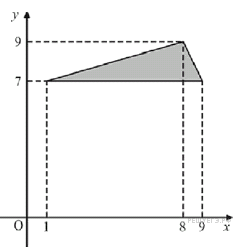
Найдите площадь треугольника, вершины которого имеют координаты (1;7) (9;7) (8;9).
56. Задание 4 № 504229. Точки D, E, F − середины сторон треугольника ABC. Периметр треугольника DEF равен 5. Найти периметр треугольника ABC.
57. Задание 4 № 505141. 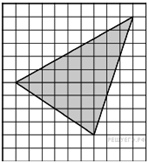 Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
58. Задание 4 № 505162. 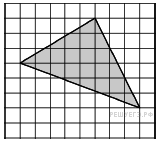 Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

 На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (9;9).
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (9;9). Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9). Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (10;9).
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (10;9). Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;7), (7;10).
Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;7), (7;10). Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8.
Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8. Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.
Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10. Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.
Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности. В треугольнике
В треугольнике  угол
угол  равен
равен  , внешний угол при вершине
, внешний угол при вершине  равен
равен  . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах. В треугольнике
В треугольнике 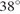 ,
,  . Найдите угол
. Найдите угол 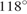 ,
,  . Ответ дайте в градусах.
. Ответ дайте в градусах. В треугольнике
В треугольнике  , угол
, угол  . Найдите внешний угол
. Найдите внешний угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.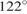 . Найдите угол
. Найдите угол  В треугольнике
В треугольнике  . Внешний угол при вершине
. Внешний угол при вершине 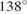 . Найдите угол
. Найдите угол  . Найдите один из других его углов. Ответ дайте в градусах.
. Найдите один из других его углов. Ответ дайте в градусах. В треугольнике
В треугольнике  ,
, 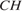 – высота, угол
– высота, угол  равен
равен 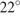 . Найдите угол
. Найдите угол 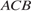 . Ответ дайте в градусах.
. Ответ дайте в градусах. В треугольнике
В треугольнике  – биссектриса, угол
– биссектриса, угол  , угол
, угол  равен
равен  . Найдите угол
. Найдите угол 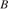 . Ответ дайте в градусах.
. Ответ дайте в градусах. В треугольнике
В треугольнике  равен
равен 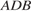 . Ответ дайте в градусах.
. Ответ дайте в градусах. В треугольнике
В треугольнике 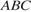
 ,
,  – высота, угол
– высота, угол 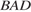 равен
равен 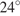 . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах. В треугольнике
В треугольнике 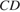 – медиана, угол
– медиана, угол  равен
равен  . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах. В треугольнике
В треугольнике 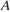 равен
равен  , а углы
, а углы 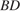 и
и  – высоты, пересекающиеся в точке
– высоты, пересекающиеся в точке 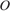 . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах. Два угла треугольника равны
Два угла треугольника равны  и
и  В треугольнике
В треугольнике 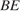 – биссектрисы, пересекающиеся в точке
– биссектрисы, пересекающиеся в точке 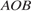 . Ответ дайте в градусах.
. Ответ дайте в градусах. Острый угол прямоугольного треугольника равен
Острый угол прямоугольного треугольника равен 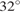 . Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах. В треугольнике
В треугольнике 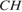 – высота,
– высота, 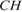 и
и  угол
угол  равен
равен 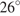 . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах. В треугольнике
В треугольнике  и
и  . Найдите меньший угол треугольника
. Найдите меньший угол треугольника  В треугольнике
В треугольнике 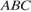 угол
угол  , угол
, угол  равен
равен 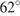 . На продолжении стороны
. На продолжении стороны  отложен отрезок
отложен отрезок  . Найдите угол
. Найдите угол 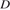 треугольника
треугольника  . Ответ дайте в градусах.
. Ответ дайте в градусах. Острые углы прямоугольного треугольника равны
Острые углы прямоугольного треугольника равны  и
и  . Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах. В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен
В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 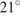 . Найдите меньший угол данного треугольника. Ответ дайте в градусах.
. Найдите меньший угол данного треугольника. Ответ дайте в градусах. Острые углы прямоугольного треугольника равны
Острые углы прямоугольного треугольника равны  и
и 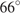 . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах. Острые углы прямоугольного треугольника равны
Острые углы прямоугольного треугольника равны  . Найдите меньший угол этого треугольника. Ответ дайте в градусах.
. Найдите меньший угол этого треугольника. Ответ дайте в градусах. В треугольнике
В треугольнике  , угол
, угол 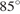 ,
, 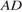 — биссектриса,
— биссектриса, 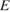 — такая точка на
— такая точка на  . Найдите угол
. Найдите угол 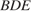 . Ответ дайте в градусах.
. Ответ дайте в градусах. В треугольнике
В треугольнике  равен
равен  равен
равен  ,
, 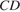 – биссектриса внешнего угла при вершине
– биссектриса внешнего угла при вершине  лежит на прямой
лежит на прямой  за точку
за точку  . Найдите угол
. Найдите угол  . Ответ дайте в градусах
. Ответ дайте в градусах В треугольнике
В треугольнике  , угол
, угол 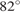 .
. 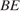 и
и 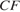 – биссектрисы, пересекающиеся в точке
– биссектрисы, пересекающиеся в точке 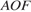 . Ответ дайте в градусах.
. Ответ дайте в градусах. В треугольнике
В треугольнике 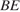 и
и 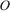 . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах. На рисунке угол 1 равен
На рисунке угол 1 равен 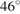 , угол 2 равен
, угол 2 равен  В треугольнике
В треугольнике  ,
,  , высота
, высота 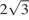 . Найдите угол
. Найдите угол  В треугольнике
В треугольнике 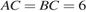 , высота
, высота  равна 3. Найдите угол
равна 3. Найдите угол  Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

 Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.


