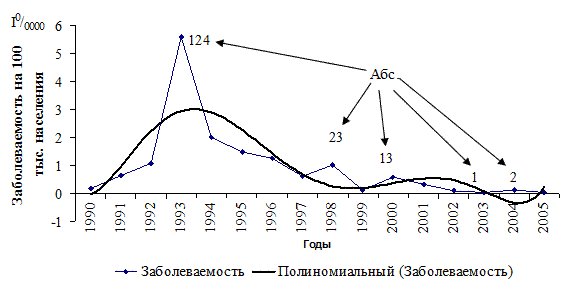
Линейные диаграммы.

Линейные диаграммы (графики) отображают количественные данные в системе координат: ось Х и ось Y. С помощью данных диаграмм отображают изменение заболеваемости во времени (их тенденции, наличие или отсутствие колебаний). В зависимости от шкалы линейные графики могут быть арифметическими (арифметическая шкала) и логарифмическими (логарифмическая шкала). Назначение линейных графиков - позволять отыскивать неизвестные промежуточные значение какой-либо величины по известным ее значениям. Арифметические графики всегда демонстративно передают абсолютные различия между показателями отдельных периодов одной кривой (рис. 1.) или показателями разных кривых (рис. 2.). При изучении динамики годовых или месячных показателей заболеваемости по арифметическим графикам необходима осторожность в формулировании даже ориентировочных выводов об особенностях тенденции и колебаний заболеваемости.

Пример арифметического графика

Рис. 1. Динамика и тенденция заболеваемости бруцеллезом в Оренбургской области за 1990 – 2005 гг. (Источник: М.В. Скачков, И.В. Ряплова Особенности эпидемического процесса бруцеллеза в Оренбургскойобласти и прогнозирования заболеваемости населения (информ-мет.письмо, 2007 г.)

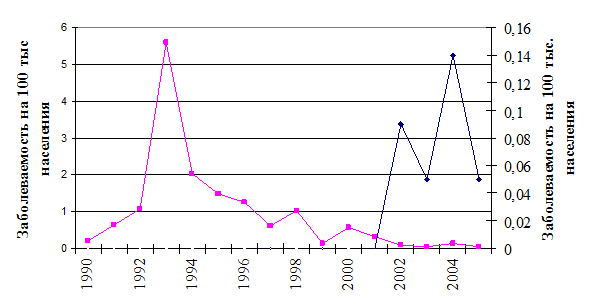
Рис. 2. Заболеваемость бруцеллезом в Домбаровском и Соль-Илецком районах Оренбургской области за 1990 – 2009 гг.

Арифметическая шкала характеризуется одинаковой длиной всех основных делений, одинаковой длиной всех промежуточных делений, значений каждого последующего основного деления отличается от предыдущего на величину цены деления. При построении графика длина по горизонтали должна быть больше длины графика по вертикали, оптимальное соотношение 1,5:1 (принцип «золотого сечения»). Данный прием значительно уменьшает субъективизм прочтения графиков, но только в тех случаях, когда показатели, отраженные на графике, существенно (на порядок и более) не отличаются друг от друга. Пересечение оси Y и оси Х происходит в точке со значением ноль. На графике должны быть представлены данные, позволяющие оценить достоверность различий, что позволяет делать выводы об особенностях тенденции и колебаний заболеваемости. На одном графике могут быть представлены две и более кривых, не отличающиеся резко друг от друга показателями (в 100 раз и более). В случае, когда на графике изображены две кривые, отличающиеся друг от друга показателями в 100 раз и более, можно рекомендовать использовать дополнительную ось Y для одной из кривой либо для части кривой (рис. 3. и 4.). Это также необходимо и для того чтобы избежать ошибочных выводов при изучении особенностей колебаний годовых показателей заболеваемости. Для большей наглядности и точных выводов целесообразно на вертикальную ось диаграмм наносить цену деления в интенсивных показателях и одновременно соответствующие им значения абсолютных чисел заболеваний. Нанесение числа заболевших позволяет понять, какое количество больных скрыто за незначительными интенсивными показателями заболеваемости без знания численности населения. Дополнительное нанесение на график числа заболевших особенно важно при необходимости изучить динамику заболеваемости отдельной, небольшой группы населения. Ограничение этого метода – существенное изменение численности населения в изучаемые годы. В этом случае абсолютные числа заболевших необходимо нанести непосредственно рядом с кривой динамики интенсивных показателей.

Пример (график с двумя осями)

.

По оси абсцисс – годы, по оси ординат – заболеваемость людей на 100 тыс.населения и количество скота в головах

Рис. 3. Связь количества больного скота и заболеваемости людей, имеющих личный скот.

Рис. 4. Заболеваемость бруцеллезом в Оренбургской области за 1990 – 2005 гг.

Для построения арифметического графика в «золотом сечении» можно использовать следующий алгоритм:

1. Выбрать длину масштабного отрезка. Длина отрезка и по оси Y и по оси X принимают равной 1 см.

2. Определить сколько масштабных отрезков необходимо отложить по горизонтали. Число масштабных отрезков по горизонтали равно числу лет исследования.

Пример, Заболеваемость бруцеллезом в Оренбургской области за 1990 – 2009 гг. число лет исследования 20, значит по оси Х мы откладываем 20 см или 20 масштабных отрезков.

3. Рассчитываем, сколько масштабных отрезков необходимо отложить по вертикали, исходя их правила «золотого сечения» Y:X=1:1,5.

Пример, длина Х=20, высота Y=20:1,5=13,3 см≈13 см. по оси Y следует отложить 13 отрезков по 1 см.

4. Рассчитываем цену деления одного масштабного отрезка по вертикали в соответствующей размерности показателя заболеваемости. Из таблицы необходимо выбрать самое большое значение показателя и разделить его на найденное число масштабных отрезков по оси Y.

В нашем примере Imax=5,6⁰/₀₀₀₀, необходимое число отрезков по оси Y=13, отсюда цена деления составляет 5,6:13=0,4⁰/_0000.

Для более точного нанесения данных на график можно воспользоваться более простым способом: заболеваемость каждого года делить на цену деления и отмерять по линейке высоту точки на графике по оси Y. Пример, заболеваемость в 2007г. составляла 0,10⁰/₀₀₀₀, следует 0,10:0,4=0,25см или 1 мм., т.е точка на носится на расстоянии 1 мм от горизонтальной оси.

Второй алгоритм построения арифметического графика по принципу «золотого сечения». Данный способ используется, когда необходимость разместить по ширине листа диаграмму, диаграмму, насчитывающую по оси Х 20 и более лет. Вначале выбираем возможную длину графика по оси Х и делим ее на необходимое количество масштабных отрезков. Далее расчет проводится как описывалось выше, начиная с пункта 3.

Если не преследуется цель выявить особенности колебаний показателей, а только необходимо сравнить величины показателей отдельных участков одной кривой или показателей разных кривых, правило «золотого сечения» можно не соблюдать.