Раздел 2. Пределы применимости закона Дарси. Нелинейные законы фильтрации

Задача № 13.

Определить значение числа Рейнольдса у стенки гидравлически несовершенной по характеру вскрытия нефтяной скважины, если известно, что эксплуатационная колонна перфорирована, на каждом ее метре простреляно 10 отверстий d₀ = 10 мм, мощность пласта h = 15 м, k = 1 Д, m = 18%, динамический коэффициент вязкости нефти m = 4 МПа×с, плотность нефти r = 870 кг/м³ и объемный дебит скважины Q = 140 м³/сут.

Ответ: Re = 15.6 (по Щелкачеву); Re = 0.396 (по Миллионщикову).

 

Задача № 14.

Определить радиус призабойной зоны r_кр, в которой нарушается закон Дарси, при установившейся плоскорадиальной фильтрации идеального газа, если известно, что приведенный к атмосферному давлению и пластовому давлению дебит скважины Q_ат = 2×10⁶ м³/сут, мощность пласта h = 10 м, проницаемость пласта k = 10 Д, пористость пласта m = 19%, динамический коэффициент вязкости m = 1.4×10^-5 кг/м×с, плотность газа при атмосферном давлении и пластовой температуре r = 0.7 кг/м³. В решении использовать в качестве R_e^(кр) нижнее значение по формуле Миллионщикова.

Ответ: r_пр = 7.9 м.

 

Задача № 15.

Определить по формуле Щелкачева, происходит ли фильтрация нефти в пласте по закону Дарси, если известно, что дебит нефтяной скважины Q = 200 м³/сут, мощность пласта h = 5 м, пористость m = 16%, проницаемость пласта k = 0.2 Д, плотность нефти r = 0.8 г/см³, динамический коэффициент вязкости m = 5 мПа×с. Скважина гидродинамически совершенна, ее радиус r_c = 0.1 м.

Ответ: R_e = 0.036 < R_e^(кр) = 1.

 

Задача № 16.

Дебит газовой скважины, приведенный к атмосферному давлению и пластовой температуре Q_ат = 2×10⁶ м³/сут, абсолютное давление на забое р_с = 7.84 МПа (80 кгс/см³), мощность пласта h = 10 м, пористость m = 18%, проницаемость k = 1.2 Д, средняя молекулярная масса M =18, динамическая вязкость газа m = 0.015 мПа×с, температура пласта t = 45⁰ С. Определить имеет ли место фильтрация по закону Дарси в призабое совершенной скважины радиусом r_с = 10 см.

 

Раздел 3. Одномерное движение несжимаемой жидкости в условиях водонапорного режима

 

Задача № 17.

Определить дебит дренажной батареи шириной В = 100 м, если мощность пласта h = 10 м, расстояние до контура питания L_k =10 км, коэффициент проницаемости k = 1 Д, динамический коэффициент вязкости жидкости m = 1 сП, давление на контуре питания р_к = 9.8 МПа (100 кгс/см²) и давление в скважинах галереи р_г = 7.35 Мпа (75 кгс/см²). Движение жидкости напорное, подчиняется закону Дарси.

Ответ: Q = 21.6 м³/сут.

 

Задача № 18.

Определить массовый дебит нефтяной скважины (в т/сут) в случае установившейся плоскорадиальной фильтрации жидкости в круговом пласте по закону Дарси, если известно, что давление на контуре р_к = 9.8 МПа (100 кгс/см²), давление на забое скважины р_с = 7.35 МПа (75 кгс/см²), проницаемость пласта k = 0.5 Д, мощность h = 15 м, диаметр скважины d_с = 24.8 см, радиус контура питания R_к = 10 км, вязкость нефти m = 6 мПа×с и плотность жидкости r = 850 кг/м³.

Ответ: Q = 127 т/сут.

 

Задача № 19.

Построить индикаторную линию (зависимость объемного дебита Q от перепада давления Dр = р_к – р_с), имеющуюся при установившейся плоскорадиальной фильтрации в круговом пласте по закону Дарси, если известно, что давление на контуре р_к = 8.82 МПа (90 кгс/см²), проницаемость пласта k = 600 мД, мощность h = 10 м, диаметр скважины d_c = 24.8 см, радиус контура питания плата R_к = 10 км и вязкость нефти m_н = 5 мПа×с.

Ответ: индикаторная линия прямая Q = 5.77 Dр (Q в м³/сут, Dр в кгс/см²).

 

Задача № 20.

Определить средневзвешенное по объему пластовое давление в круговом пласте - P_ср, если известно, что давление на контуре пласта р_к = 9.8 МПа (100 кгс/см²), давление на забое скважины р_с = 7.84 МПа (80 кгс/см²), радиус контура питания пласта R_к = 25 км, радиус скважины r_с = 10 м. В пласте имеет место установившееся плоскорадиальное движение несжимаемой жидкости по закону Дарси.

Ответ: P_ср = 9.72 МПа (99.19 кгс/см²).

 

Задача № 21.

Определить относительное понижение S_р/S = пьезометрического уровня в реагирующих скважинах, расположенных от возмущающей на расстояниях r =1 м, 100 м, 1 км, 10 км. Движение жидкости установившееся плоскорадиальное по закону Дарси, радиус скважины r_с = 0.1 м, радиус контура питания пласта R_к = 100 км.

Ответ: S_p/S = 0.83; 0.50; 0.33; 0.161.

 

Задача № 22.

Определить время T отбора нефти из призабойной зоны скважины радиусом r₀ = 100 м, если мощность пласта h = 10 м, пористость m = 20%, массовый дебит скважины Q_m = 40 т/сут, плотность нефти r = 920 кг/м³, радиус скважины r_с = 0.1 м.

Ответ: Т = 1440 сут.

 

Задача № 23.

Определить время t, за которое частица жидкости подойдет к стенке скважины с расстояния r₀ = 200 м, если проницаемость пласта k = 1 Д, динамическая вязкость жидкости m = 5сП, депрессия во всем пласте радиусом R_к = 1 км составляет р_к – р_с = 10 кгс/см², мощность пласта h = 10 м, пористость m = 15%, радиус скважины r_с = 10 см.

Ответ: t = 1600 сут.

 

Задача № 24.

Во сколько раз необходимо увеличить радиус скважины, чтобы ее дебит в круговом пласте при прочих равных условиях удвоился?

1) движение жидкости происходит по закону Дарси;

2) движение жидкости происходит по закону Краснопольского.

Начальный радиус скважины r_с = 0.1 м. Расстояние до контура питания пласта R_к = 1 км.

Ответ: 1) n = 100, r¹_c = 10 м;

2) n = 4, r¹_c = 0.4 м.

 

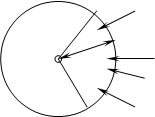
Задача № 25.

Скважина r_с = 10 см расположена в центре кругового пласта с радиусом контура питания R_к = 350 м, проницаемость пласта k = 0.8 Д, мощность h = 12 м, вязкость несжимаемой жидкости m = 5 сП. Определить дебит скважины, считая, что ее залежь по контуру частично непроницаема. Контур питания – дуга окружности радиуса R_к с центральным углом a = 120⁰. Давление на контуре питания р_к = 27.9 МПа (285 кгс/см²); давление на скважине р_с = 7.84 МПа (80 кгс/см²).

(Дооформить рис)

 

 

Задача № 26.

Какой объем жидкости следует закачивать в пласт в единицу времени через нагнетательную скважину, если необходимо чтобы давление в скважине поддерживался в процессе закачки на Dр = 1.47 МПа (15 кгс/см²) выше давления, установившегося в пласте на расстоянии r = 2 км от скважины? Имеет место закон Дарси. Динамическая вязкость жидкости m = 1 сП, проницаемость пласта k = 150 мД, мощность h = 10 м, радиус скважины r_с = 10 см.

Ответ: Q = 123 м³/сут.

 

Задача № 27.

Скважина вскрывает пласт бесконечно большой мощности на небольшую глубину. Считая движение радиально-сферическим, определить время t перемещения частиц жидкости вдоль линий тока от точки с координатой r_о = 100 м до r = 5 м. Скважина эксплуатируется с постоянным объемным дебитом Q = 120 м³/сут, коэффициент пористости пласта m = 15%.

Ответ: t = 7.15 лет.