Раздел 5. Установившаяся фильтрация сжимаемой жидкости и газа
Задача № 48. Определить проницаемость песка, если через трубу диаметром d = 200 мм и длиной l = 12 м, заполненную песком, пропускается воздух динамической вязкостью m =0.018 мПа×с при перепаде давления, равном Dр =4.41×104 Па (0.45 кгс/см2); избыточное давление в начале и конце трубы составляют соответственно р1 = 0.98×105 Па и р2 = 0.539×105 Па (0.55 кгс/см2). Средний расход воздуха, приведенный к атмосферному давлению, равен Q =250 см3/с. Атмосферное давление принять равным рат = 0.98×105 Па, температура t = 200С. Ответ: k = 21.5 Д.
Задача № 49.
Задача № 50. В пласте имеет место установившаяся плоскорадиальная фильтрация газа по закону Дарси. Абсолютное давление на контуре питания рк = 9.8 МПа (100 кгс/см2), давление на забое скважины рс = 68.6 МПа (70 кгс/см2), приведенный к (рат, Тпл) объемный расход газа Qа т = 8×105 м3/сут. Радиус контура питания Rк = 750 м, радиус скважины rс = 0.1 м, мощность пласта h = 10 м, пористость m = 20%. Определить пластовое давление р, скорость фильтрации w и и среднюю скорость движения u на расстоянии r = 50 м от скважины. Ответ: р = 9.02 МПа; w = 3.32×10-5 м/с; u = 1.66×10- 4 м/с.
Задача № 51. Определить расстояние r¢ от возмущающей газовой скважины до точки пласта, в которой давление равно среднеарифметическому от забойного давления рс = 70 кгс/см2 и давления на контуре рк = 100 кгс/см2, если расстояние до контура питания Rк = 1000 м, радиус скважины rс = 0.1 м. Ответ: r¢ = 6.76 м.
Задача № 52. Определить объемный приведенный к атмосферному давлению (Qат) и массовый (Qm) дебиты совершенной газовой скважины, считая, что фильтрация проходит по закону Дарси, если: мощность пласта h = 25 м, проницаемость k = 250 мД, динамическая вязкость газа m = 0.014 мПа×с; плотность газа в нормальных условиях rат = 0.650 кг/м3, радиус скважины rс = 0.1 м, радиус контура питания Rк = 900 м; абсолютное давление на забое скважины рс = 2.94 МПа и на контуре питания рк = 3.92 МПа. Газ считать идеальным. Ответ: Qm = 607 т/сут; Qат = 0.935×103 м3/сут.
Задача № 53. Известно, что в круговом пласте происходит установившаяся плоскорадиальная фильтрация газа по закону Дарси. Радиус контура питания Rк = 1000 м, радиус скважины rс = 0.1 м, давление на контуре рк = 100 кгс/см2, давление на забое скважины рс = 92 кгс/см2. Определить средневзвешенное давление в пласте и показать, что оно близко к контурному- рк.
Задача № 54. Показать, что при установившемся прямолинейном параллельном движении газа в пористой среде в условиях напорного режима распределение давления в пласте не описывается законом фильтрации, выраженным в виде одночленной степенной формулы
Задача № 55. Найти коэффициенты А и В уравнения индикаторной кривой по данным испытания газовой скважины, приведенным в таблице
Задача № 56. Природный газ имеет следующий состав:
Определить дебит Qат газовой скважины, учитывая реальные свойства газа и сравнить его с дебитом Q¢ат для идеального газа. При решении использовать график коэффициентов сверхсжимаемости z от приведенной температуры и давления и график динамической вязкости m (р,r)t=38оС. Статическое давление на забое принимается за контурное рк = 150 кгс/см2; динамическое за давление в скважине рс = 100 кгс/см2, коэффициент проницаемости пласта k = 0.1 Д, мощность пласта h = 10 м, радиус контура области дренирования Rк = 1 км, радиус скважины rс = 10 см.
|



 Используя принцип однородности размерностей, можно найти выражение для С
Используя принцип однородности размерностей, можно найти выражение для С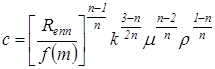 , где f(m) = 10m-2/3?
, где f(m) = 10m-2/3?


