Решение. Т.к. шары в каждом опыте возвращаются обратно и перемешиваются, то испытания можно считать независимыми (результат предыдущего опыта не влияет на вероятностьТ.к. шары в каждом опыте возвращаются обратно и перемешиваются, то испытания можно считать независимыми (результат предыдущего опыта не влияет на вероятность появления или не появления события в другом опыте). Таким образом, вероятность появления белого шара в каждом опыте постоянна и равна 1) Белый шар не появился вовсе: 2) Белый шар появился один раз: 3) Белый шар появиться два раза: 4) Белый шар появиться три раза: 5) Белый шар появиться четыре раза: 6) Белый шар появился пять раз: Получаем закон распределения случайной величины
Найдем математическое ожидание
Вычислим дисперсию
Ответ:
|
, соответственно, вероятность появления черного шара 
. Значит, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз. Для составления закона распределения надо найти вероятности каждого из этих событий. Для этого будем использовать формулу Бернулли 
.
.
.
.
.
.
.
.
:
.
,
,
.
; 
.
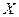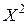
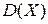
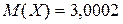