Дифференциальное уравнение неразрывности потока выведено в параграфе 1.4. Если происходит установившееся фильтрация, то в этом уравнении производная по времени будет равна нулю. Если жидкость несжимаема, а пористая среда недеформируемая и однородна, то плотность, вязкость жидкости и проницаемость пласта постоянны и их можно вынести из-под знака дифференциала и уравнение неразрывности примет вид:
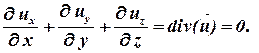
| (2.1)
|
Подставим в это уравнение скорости фильтрации, найденные из закона Дарси (п. 1.2), получим дифференциальное уравнение установившегося движения:

| (2.2)
|
Это уравнение называется уравнением Лапласа. Уравнение Лапласа – линейное дифференциальное уравнение так, как сумма решений уравнения Лапласа также является решением этого уравнения. На этом свойстве основан метод суперпозиции (наложения) решений, который будет использоваться в дальнейшем.
В случае притока к галерее, уравнение Лапласа запишется:
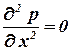 . .
| (2.3)
|
а для скважины
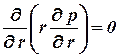 . .
| (2.4)
|
Для простых фильтрационных потоков установившегося движения несжимаемой жидкости уравнение неразрывности удобно записывать в интегральном виде:
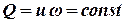 . .
| (2.5)
|
Одномерные фильтрационные потоки

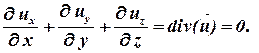

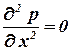 .
.
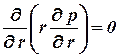 .
.
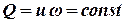 .
.



