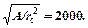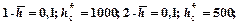Прямоугольной формы за счет напора подошвенной воды
Делаются следующие предположения: 1. Пласт представляется параллелепипедом с квадратной площадью дренажа А, постоянной толщиной h и пористостью т; проницаемостью по горизонтали и вертикали соответственно K и Kz; скважина радиуса r с расположена в центре дренируемой площади и вскрывает пласт частично на величину b. 2. Жидкость однофазная малосжимаемая с коэффициентом сжимаемости b ж, вязкость жидкости m, расход Q = const. 3. Первоначальное давление Р 0в пласте всюду одинаково; при непроницаемых кровли и внешнем контуре на подошве пласта поддерживается постоянное давление равное начальному; гравитационные силы не учитываются, что вполне допустимо, так как рассматривается однофазный приток. Таким образом, задача сводится к решению уравнения пьезопроводности (8.2.5) при следующих начальных и граничных условиях согласно схемы рис. 8.1:
Последнее условие в (8.3.2) указывает, что давление в скважине не зависит от координаты Z (условие постоянства потенциала вдоль вскрытой части пласта), а условие (8.3.3) утверждает постоянство дебита скважины. Символ r есть расстояние по радиусу относительно оси скважины. Существуют различные методы решения задач для распределения давления в пласте, дренируемого несовершенной скважиной. Например, методы: стоков-источников, интегральное преобразование, функции Грина, конечных разностей, конечных элементов, фильтрационных сопротивлений и термодинамических аналогий. Все аналитические решения предполагают, что жидкость из пласта поступает в скважину с одинаковой плотностью расхода по вскрытой части, что, дает возможность на основании последнего равенства в (8.3.2) условие (8.3.3) переписать в виде
Решение, удовлетворяющее условию (8.3.4), известно как решение для постоянного расхода. Грингартен и Рамей показали [29], что такое решение может быть использовано для определения падения давления на скважине с помощью численных методов, которое удовлетворяет постоянству потенциала на скважине и постоянству расхода (8.3.3). Автор [29] делает расчет падения давления на забое (депрессии) по особой точке в интервале вскрытия пласта. Для несовершенной скважины по степени вскрытия расположение этой точки зависит от параметра Строго говоря, условия (8.3.3) и (8.3.4) справедливы для линии стоков-источников. Однако многими исследователями показано, что реальную скважину можно принять за линейный сток с достаточным обоснованием. Рассматриваемую здесь задачу Бухидма [29] решал с использованием функции Грина и функций мгновенных стоков-источников, разработанных Грингартеном и Рамеем [29]. Для понижения давления на забое скважины (депрессии) при х 0= у 0получено следующее уравнение в безразмерном виде (в наших символах с некоторыми преобразованиями):
где
m – коэффициент пористости; В – объемный коэффициент жидкости. Уравнение (8.3.5) затабулировано [28]. Графические зависимости
Рис. 8.2. Графические зависимости функции безразмерной депрессии для притока к несовершенной скважине, дренирующей однородно-анизотропный пласт прямоугольной формы с подошвенной водой, при параметрах:. 1—0,1; 2—0,2; 3—0,3; 4—0,4; 5—0,5; 6—0,6; 7—0,7; 8—0,8; 9—0,9; 10—1
Здесь положение особой точки Z c зависит от интервала вскрытия
где
А = Х 0 Y 0 – площадь дренирования (см. рис. 8.1). Уравнение (8.3.8) справедливо при
Рис. 8.3. Графические зависимости функции безразмерной депрессии 1—0,9; 2—10-1; 3—10-2; 4—10-3; 5—10-4; 6—10-5; 7—10-6. 8.3.2. Определение средневзвешенного давления в пласте. Расчет средневзвешенного по объему дренирования пластового давления основывается на материальном балансе запасов углеводородов V. Математически для безразмерного давления
Внося (8.3.5) в (8.3.10) и интегрируя [29], получаем
Для раннего периода времени влиянием притока жидкости в пласт можно пренебречь. Тогда для среднего давления имеем В заключение можно отметить следующее. Приведенное здесь уравнение для несовершенной линии стоков, частично вскрывающей однородно-анизотропный пласт с непроницаемыми границами, имеющий в горизонтальном сечении форму квадрата, с напором подошвенных вод постоянного давления на границе раздела вода–нефть, может быть использовано для решения как прямых, так и обратных задач подземной гидродинамики. Анализ зависимости безразмерного давления от безразмерного времени показывает наличие трех режимов течения: ранний неустановившийся, неустановившийся и установившийся периоды. Heустановившийся период не соответствует периоду псевдорадиального притока. Это означает, что информация об относительном вскрытии и коэффициенте продуктивности не может быть получена обычными методами анализа изменения забойного давления. Также не может быть определена и вертикальная проницаемость по методам, базирующимся на предположении существования периода псевдорадиального притока, если явно доминирует напор подошвенных вод. Продуктивность вскрытого интервала может быть определена по зависимости
Рис. 8.4. Зависимость безразмерного средневзвешенного давления
Заметим, использование приведенных здесь аналитических решений для интерпретации результатов гидродинамических исследований скважин детально рассмотрено в работе [29]. В формулах (8.3.6) и (8.3.9) принимаются следующие размерности физических величин: [ K ]=Да, [ h ]=м, [ Q ]=м3/c, [ B ]=м3/м3, [ m ]=Па×с, [ Р ]=КПа, [ b* ]=1/КПа, [ А ]=м2, [ t ]=c, [ r c]=м.
|

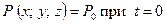 ; (8.3.1)
; (8.3.1) (8.3.2)
(8.3.2)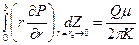 . (8.3.3)
. (8.3.3)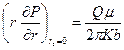 . (8.3.4)
. (8.3.4) . Подобный прием отыскания аналогичной точки был также использован Грингартеном [29] при дренировании пласта бесконечной вертикальной трещиной.
. Подобный прием отыскания аналогичной точки был также использован Грингартеном [29] при дренировании пласта бесконечной вертикальной трещиной.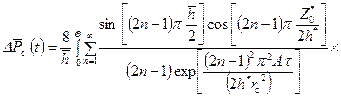
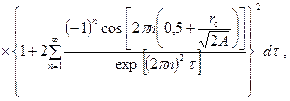 (8.3.5)
(8.3.5) ; (8.3.6)
; (8.3.6) , (8.3.7)
, (8.3.7) представлены на рис. 8.2 и 8.3.
представлены на рис. 8.2 и 8.3.
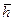 , метод отыскания которой изложен в работе [29]. Многими исследователями показано, что поведение функции давления в начальный период времени описывается уравнением:
, метод отыскания которой изложен в работе [29]. Многими исследователями показано, что поведение функции давления в начальный период времени описывается уравнением: , (8.3.8)
, (8.3.8)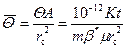 ; (8.3.9)
; (8.3.9)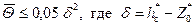 ;
;  . Оно показывает, что в начальный период времени поведение несовершенной скважины такое же, как и совершенной скважины, дренирующий пласт на полную толщину h.
. Оно показывает, что в начальный период времени поведение несовершенной скважины такое же, как и совершенной скважины, дренирующий пласт на полную толщину h.
 для притока к несовершенной скважине, дренирующей однородно-анизотропный пласт прямоугольной формы с подошвенной водой, при параметрах:
для притока к несовершенной скважине, дренирующей однородно-анизотропный пласт прямоугольной формы с подошвенной водой, при параметрах:  .
.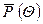 справедливо
справедливо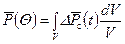 . (8.3.10)
. (8.3.10) . (8.3.11)
. (8.3.11) . Уравнение (8.3.11) справедливо, строго говоря, для однородного потока жидкости в ограниченном пласте. Но поскольку различие в решениях между указанным потоком и потоком в бесконечном пласте носит лишь локальное значение (в призабойной зоне), то решение (8.3.11) может быть использовано и для неограниченного пласта [29]. Расчетные значения безразмерного средневзвешенного давления по уравнению (8.3.11) для некоторых случаев приведены на рис. 8.4 [29]. Как видно из графиков, для раннего периода времени зависимость
. Уравнение (8.3.11) справедливо, строго говоря, для однородного потока жидкости в ограниченном пласте. Но поскольку различие в решениях между указанным потоком и потоком в бесконечном пласте носит лишь локальное значение (в призабойной зоне), то решение (8.3.11) может быть использовано и для неограниченного пласта [29]. Расчетные значения безразмерного средневзвешенного давления по уравнению (8.3.11) для некоторых случаев приведены на рис. 8.4 [29]. Как видно из графиков, для раннего периода времени зависимость  является линейной. Время, при котором кривые отклоняются от прямой линии, представляет собой начало неустановившегося процесса в пласте и является функцией параметров
является линейной. Время, при котором кривые отклоняются от прямой линии, представляет собой начало неустановившегося процесса в пласте и является функцией параметров  . Как видно из графика (см. рис. 8.4), это время увеличивается с увеличением
. Как видно из графика (см. рис. 8.4), это время увеличивается с увеличением 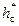 и уменьшением
и уменьшением 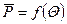 в ранний неустановившийся период при выполнении условия
в ранний неустановившийся период при выполнении условия 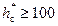 . Если выполняется условие
. Если выполняется условие 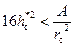 то зависимость
то зависимость 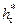 существует минимальная площадь дренажа вдали от скважины, где эффект непроницаемых боковых границ не наблюдается. Если выполняется условие
существует минимальная площадь дренажа вдали от скважины, где эффект непроницаемых боковых границ не наблюдается. Если выполняется условие 
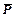 от безразмерного времени Θ; для замкнутого пласта с напором подошвенной воды, дренирующего с несовершенной кважиной, расположенной в центре квадрата при относительной площади дренирования
от безразмерного времени Θ; для замкнутого пласта с напором подошвенной воды, дренирующего с несовершенной кважиной, расположенной в центре квадрата при относительной площади дренирования