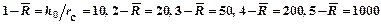Методика расчета фильтрационных сопротивлений при неустановившемся осесимметричном притоке жидкости (газа) к несовершенной скважине в неограниченном пласте.
В Гл. 8 приведено решение (8.2.27) для неустановившегося притока сжимаемой жидкости к несовершенной скважине в однородно-анизотропном неограниченном по протяженности пласте по линейному закону фильтрации. Это решение может быть использовано для определения понижения давления на забое скважины после ее пуска, повышения давления на забое после остановки скважины, а также с целью анализа распределения потенциала (давления) в пласте во время работы скважина. Трудность использования указанного уравнения для практических целей заключается в его сложности. В приведенном виде решение не может быть попользовано для инженерных задач по двум причинам. Во-первых, функция (8.2.27) очень сложная и требует своего табулирования. Во-вторых, вид такой функции исключает возможность выделить время в качестве слагаемого в решении (8.2.27) и свести его к уравнению прямой, что необходимо для интерпретации кривых понижения или восстановления давления в скважинах традиционными методами. Чтобы избежать упомянутых трудностей, можно поступить следующим образом. Как известно, в теории и практике гидродинамических исследований широко используется интегральная показательная функция. Несовершенство скважины при этом учитывается путем введения добавочных фильтрационных сопротивлений С1, взятых из решения задач для установившегося притока. Насколько такое допущение правильно, пока еще ни теоретически, ни экспериментально не доказано. Сведем функцию (8.2.27) к интегральной показательной и произведем расчет функции сопротивления (аналог добавочного сопротивления С1) при неустановившемся притоке, зависящей не только от геометрии пласта, но и от параметра Фурье (f 0).
9.3.1. Обоснование функции фильтрационного сопротивления. За основу возьмем функцию (8.2.28). Следовательно, для условий на забое
С другой стороны, запишем следующее выражение:
Решая совместно (9.3.1) и (9.3.2), находим
или
Анализ показывает следующее. Равенство (9.3.4) содержит в себе интеграл вероятности Ф (х) и ряд
Для расчета на ЭВМ функции сопротивления (9.3.4) требуется рассмотреть поведение (9.3.5), определить правило вычисления интеграла вероятности и выяснить условия его сходимости при заданных значениях f 0, Интеграл вероятности, определяемый как
для всех значений
Число используемых членов ряда определялось из соотношения
Для значений
где а 0=1; а 1=0,07052308; а 2=0,04228201; а 3=0,009270527; а 4=0,0001520143; а 5=0,0002765672; а 6=0,000430638; для всех Интеграл вероятности – это ограниченная, монотонно возрастающая функция на интервале от 0 до ¥. Тогда при некотором п будет выполнено условие [27]
Это будет допустимо, когда
Разрешая неравенство (9.3.11) относительно п, находим число членов ряда (9.3.5). Интеграл (9.3.1) при Расчет безразмерной депрессии
9.3.2. Сопоставление значений добавочных фильтрационных сопротивлений для установившегося и квазинеустановившегося притоков. Анализы показали, что при Нами произведены сопоставления значений функции сопротивления R ( Заметим, что в условиях взаимодействия несовершенных нефтяных и газовых скважин при линейном и нелинейном законах фильтрации формулы и методика расчета фильтрационных сопротивлений, приведенные здесь, остаются справедливыми. Подводя итоги изложенному, можно сделать следующие выводы: – Численные значения функции – Численные значения функции фильтрационного сопротивления – Численные значения функции фильтрационного сопротивления – Полученное аналитическое решение для неустановившегося притока сжимаемой жидкости (газа) к несовершенной скважине в бесконечном по протяженности пласте преобразовано в прямолинейную анаморфозу, которая позволяет эффективно производить интерпретацию кривых восстановления забойного давления; – Предложенный здесь прием преобразования уравнения притока в интегральной форме (9.3.1), произведенные расчеты и табулирование функций
Рис.9.9. Характеристика изменения функции фильтрационного сопротивления при параметре
Рис. 9.10. Сопоставление значений функции сопротивления
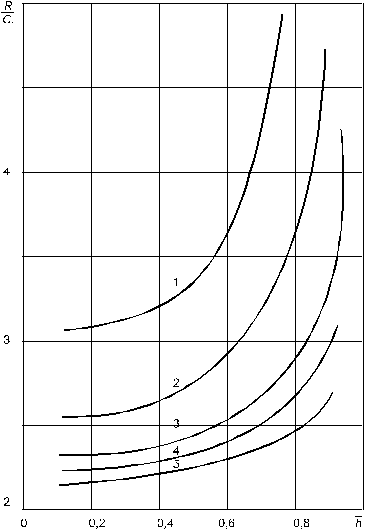
Рис. 9.11. Зависимость отношения
|

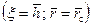 интеграл (8.2.27) примет вид:
интеграл (8.2.27) примет вид: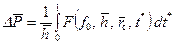 . (9.3.1)
. (9.3.1)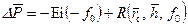 . (9.3.2)
. (9.3.2)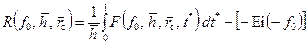 (9.3.3)
(9.3.3)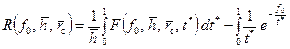 . (9.3.4)
. (9.3.4)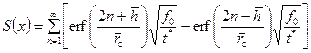 . (9.3.5)
. (9.3.5)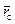 ,
,  , t *.
, t *. (9.3.6)
(9.3.6)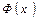 <1, вычислялся с помощью ряда
<1, вычислялся с помощью ряда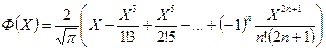 . (9.3.7)
. (9.3.7)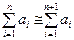 . (9.3.8)
. (9.3.8)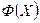 <3,767 использовалось аппроксимирующее выражение:
<3,767 использовалось аппроксимирующее выражение: , (9.3.9)
, (9.3.9) ряда (9.3.5) лежит в пределах:
ряда (9.3.5) лежит в пределах: 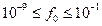 ;
; 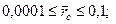
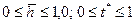 . Так как значения параметров
. Так как значения параметров  фиксированы, то ряд (9.3.5) зависит только от п. Члены рассматриваемого ряда представляют собой разность интегралов вероятности.
фиксированы, то ряд (9.3.5) зависит только от п. Члены рассматриваемого ряда представляют собой разность интегралов вероятности.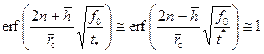 . (9.3.10)
. (9.3.10)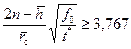 . (9.3.11)
. (9.3.11)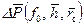 и функции сопротивления
и функции сопротивления 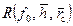 производился соответственно по формулам (9.3.1) и (9.3.4) на БСМ-Минск-32, ОС “Фортран” в СибНИИНП объединения “Главтюменнефтегаз” В.И. Леоновым. Для расчета был разработан алгоритм. Параметры менялись в широком диапазоне:
производился соответственно по формулам (9.3.1) и (9.3.4) на БСМ-Минск-32, ОС “Фортран” в СибНИИНП объединения “Главтюменнефтегаз” В.И. Леоновым. Для расчета был разработан алгоритм. Параметры менялись в широком диапазоне: 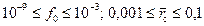 ;
; 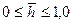 . Функция
. Функция 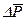 (9.3.1) затабулирована (см. Прил. 1 [28]); расчетные значения
(9.3.1) затабулирована (см. Прил. 1 [28]); расчетные значения 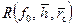 приведены в Прил. 2.
приведены в Прил. 2.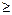 0,10 для любого
0,10 для любого 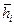 функция сопротивления не зависит от параметра Фурье f 0, а зависит только от геометрии пласта (рис. 9.9). При
функция сопротивления не зависит от параметра Фурье f 0, а зависит только от геометрии пласта (рис. 9.9). При 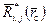 также не зависит от
также не зависит от 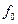 , что свидетельствует о квазиустановившемся притоке. Как уже упоминалось ранее, в нефтегазопромысловой практике расчетов, связанных с неустановившемся притоком и учетом несовершенства скважин, принимаются значения фильтрационных сопротивлений, относящихся к установившемуся притоку в ограниченном пласте. Приемлемость этого допущения пока еще не обоснована.
, что свидетельствует о квазиустановившемся притоке. Как уже упоминалось ранее, в нефтегазопромысловой практике расчетов, связанных с неустановившемся притоком и учетом несовершенства скважин, принимаются значения фильтрационных сопротивлений, относящихся к установившемуся притоку в ограниченном пласте. Приемлемость этого допущения пока еще не обоснована.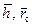 ) для квазиустановившегося притока при f 0=10
) для квазиустановившегося притока при f 0=10 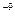 созначениями добавочных фильтрационных сопротивлений
созначениями добавочных фильтрационных сопротивлений 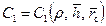 при
при 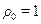 для установившегося притока в ограниченном пласте. Графические зависимости
для установившегося притока в ограниченном пласте. Графические зависимости 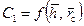 и
и 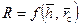 (рис. 9.10), а также
(рис. 9.10), а также 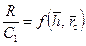 (рис. 9.11) показывают, что всюду значения функции сопротивления превосходят значения фильтрационных сопротивлений при установившемся притоке (R>C 1). Например, при
(рис. 9.11) показывают, что всюду значения функции сопротивления превосходят значения фильтрационных сопротивлений при установившемся притоке (R>C 1). Например, при  =1000 и R / С 1=3,47 для
=1000 и R / С 1=3,47 для 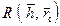 и
и  аналогичный (см. рис. 9.9-9.11).
аналогичный (см. рис. 9.9-9.11).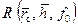 для неустановившегося притока при любом вскрытии пласта всегда меньше численных значений фильтрационных сопротивлений
для неустановившегося притока при любом вскрытии пласта всегда меньше численных значений фильтрационных сопротивлений  при квазиустановившемся движении;
при квазиустановившемся движении;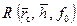 для неустановившегося и квазиустановившегося притоков превосходят в несколько раз значения добавочных фильтрационных сопротивлений
для неустановившегося и квазиустановившегося притоков превосходят в несколько раз значения добавочных фильтрационных сопротивлений 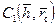 для установившегося притока в однородном ограниченном пласте; значений фильтрационных сопротивлений
для установившегося притока в однородном ограниченном пласте; значений фильтрационных сопротивлений  при квазиустановившемся движении;
при квазиустановившемся движении; для установившегося притока в однородном ограниченном пласте;
для установившегося притока в однородном ограниченном пласте;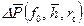 и
и 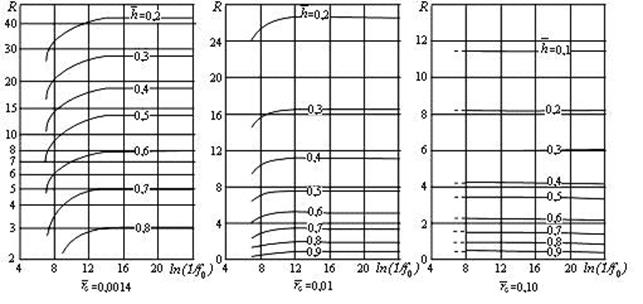
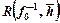
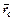

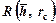 для квазиустановившегося притока при f 0=10-9 со значениями добавочных фильтрационных сопротивлений для установившегося притока
для квазиустановившегося притока при f 0=10-9 со значениями добавочных фильтрационных сопротивлений для установившегося притока 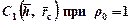
 при параметрах:
при параметрах: