Для притока к несовершенной скважине, дренирующей однородно-анизотропный
пласт прямоугольной формы с подошвенной водой, при параметрах:
Линейная анаморфоза этого уравнения для кривой восстановления давления есть
где
Р с(t р) — забойное давление в момент остановки скважины t р ; Р с(t) — восстановленное забойное давление. Построив КВД в координатах { Если период работы скважины до остановки t p соизмерим с периодом наблюдения t после остановки, тогда по принципу суперпозиции получаем обобщенное уравнение Хорнера:
где
Построив кривую в координатах
9.4.2. Несовершенная скважина дренирует однородно-анизотропный пласт цилиндрической формы при упруговодонапорном режиме. Решение задачи о понижении давления в однородно-изотропном круговом пласте при работе центральной совершенной скважины в условиях упруговодонапорного режима впервые дано Маскетом [1] в виде:
где функция
Впоследствии В.А. Щелкачевым [19] было указано, что формула (9.4.9) приемлема для практических расчетов при
При анализе основных модельных задач исследования газовых скважин Г.А. Зотов и С.М. Тверковкин [9] отметили достаточно высокую точность приближенной аппроксимации для практических расчетов. Однако следует отметить довольно значительное расхождение в результатах расчетов функции Представим аналитическое решение (8.6.9) для понижения давления на забое скважины через функцию сопротивления
Решая совместно (8.6.9) и (9.4.11), получаем:
где функции Х, Y и F выражаются соответственно формулами (8.6.10), (8.6.11).Функцию
|

 ,
,  ,
,  .
.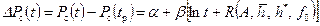 , (9.4.4)
, (9.4.4)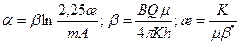 ; (9.4.5)
; (9.4.5)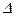 Р с(t);
Р с(t);  }, по прямолинейному участку ее можно определить угловой коэффициент
}, по прямолинейному участку ее можно определить угловой коэффициент  и отрезок
и отрезок 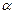 , отсекаемый на оси ординат. Затем по формулам (9.4.5) нетрудно определить коэффициенты гидропроводности и пьезопроводности пласта.
, отсекаемый на оси ординат. Затем по формулам (9.4.5) нетрудно определить коэффициенты гидропроводности и пьезопроводности пласта. , (9.4.6)
, (9.4.6) . (9.4.7)
. (9.4.7)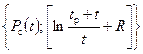 , можно определить путем экстраполяции прямой до значения
, можно определить путем экстраполяции прямой до значения  (при
(при 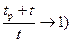 среднепластовое давление Р пл, а по угловому коэффициенту
среднепластовое давление Р пл, а по угловому коэффициенту  , (9.4.8)
, (9.4.8)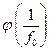 представляется бесконечным рядом через функцию Бесселя. И.А. Чарный предложил простую экспоненциальную аппроксимацию указанной функции вида
представляется бесконечным рядом через функцию Бесселя. И.А. Чарный предложил простую экспоненциальную аппроксимацию указанной функции вида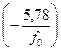 . (9.4.9)
. (9.4.9)
 0,15. Г.И. Баренблатт [43] получил наиболее точную формулу вида
0,15. Г.И. Баренблатт [43] получил наиболее точную формулу вида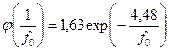 . (9.4.10)
. (9.4.10) по формулам (9.4.9) и (9.4.10). Так формула (9.4.10) занижает результаты: при
по формулам (9.4.9) и (9.4.10). Так формула (9.4.10) занижает результаты: при  на 23,5%; при
на 23,5%; при  на 53,8% и при
на 53,8% и при  на 78,8%.
на 78,8%. , основываясь на решении (9.4.8) для притока к несовершенной скважине:
, основываясь на решении (9.4.8) для притока к несовершенной скважине:
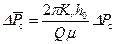 . (9.4.11)
. (9.4.11) , (9.4.12)
, (9.4.12)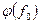 рекомендуется вычислять по формуле И.Г. Баренблатта (9.4.10). Ясно, что реализация решения (9.4.12) требует табулирования функции сопротивления R.
рекомендуется вычислять по формуле И.Г. Баренблатта (9.4.10). Ясно, что реализация решения (9.4.12) требует табулирования функции сопротивления R.


