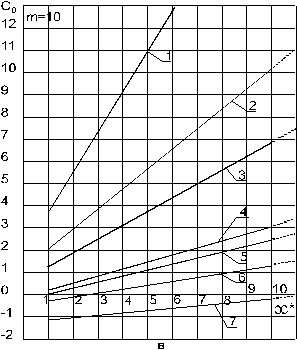Методика расчета фильтрационных сопротивлений, обусловленных перфорацией колонны
9.5.1. Краткая история вопроса. Приток к несовершенной скважине только по степени вскрытия (с открытым забоем) достаточно хорошо изучен как аналитически, так и экспериментально. Большие аналитические трудности представляют задачи о притоке жидкостей или газа к скважине, обсаженной и перфорированной. Впервые эта задача в приближенной постановке решена М. Маскетом [1, 1943]. Затем последовала работа М.Н. Тихова [2, 1947] и А.Л. Хейна [3, 4, 1953], которые рассмотрели задачу о притоке жидкости и газа к скважинам, несовершенным по характеру и степени вскрытия при условии существования меридиально симметричных поверхностей перфорации. В 1964 г вышла в свет книга М.Н. Тихова [2], в которой изложена математическая теория притока жидкости к несовершенной по характеру вскрытия пласта скважине и построена метрическая теория интерференции малых отверстий. Обоснован также закон существования оптимального числа отверстий, превышение которого уже не приводит к существенному возрастанию дебита. Решения оказались весьма сложные, почему и не получили до сих пор практической реализации, несмотря на широкое использование ЭВМ в настоящее время. Автор не дал в монографии доступных инженерных решений. Наша попытка использовать приведенные автором аналитические решения [2] для практических целей результата не дала. Например, для самого простейшего случая, когда имеется одно отверстие в колонне, следует формула для дебита:
где
(r c G – функция, представляемая суммой из пяти слагаемых, выраженных бесконечными рядами, включающими некоторые сложные функции Т, С и S [2]; h 0 – продуктивная толщина пласта; S 0= r c Как видно, реализация формулы (9.5.2) для практических целей невозможна. Кроме того, формула (9.5.2) не учитывает глубину канала. Широко известные графические зависимости дополнительных фильтрационных сопротивлений от соответствующих параметров, обусловленных перфорацией, полученные В.И. Щуровым по результатам электролитического моделирования и М.Х. Харрисом – по результатам математического моделирования [35], также имеют известные ограничения (недостаточный диапазон исходных параметров, графическая приближенность определения, не учет анизотропии и др.). Наиболее простой и практически приемлемой для дебита перфорированной скважины является формула [44]
полученная на основе решения Ю.П. Борисова, В.П. Пилатовского и В.П. Табакова. Формула (9.5.3) справедлива для любой схемы вскрытия (кроме спирального расположения перфорационных каналов) при условии, что каждый из m перфорационных каналов длиной l 0 и радиусом r 0ограничен m горизонтальными плоскостями с одинаковыми расстояниями между отверстиями и плоскостями. Здесь m – плотность перфорации, [ m ]=1/м.
9.5.2. Многозонная схема притока к перфорированной скважине. Рассмотрим эту задачу в более общей постановке: пласт однородно-анизотропный, горизонтальный, ограниченный непроницаемыми кровлей и подошвой с конечным радиусом r к контура питания; скважина экранированная, несовершенная по степени и характеру вскрытия (см. рис. 9.3). Используя многозонную схему притока к единичному каналу, для соответствующих зон можно записать следующие формулы притока через потенциалы Ф с учетом верхних т горизонтальных плоскостей:
b – вскрытие пласта обсаженной колонной, перфорированной т каналами, каждый из которых приходится на один интервал между двумя плоскостями; l 0 – длина канала, отсчитываемая от оси скважины. В силу неразрывности потока дебиты, определяемые формулами (9.5.4) и (9.5.5), равны. Тогда, производя некоторые преобразования, по правилу производных пропорций из (9.5.4) и (9.5.5) получаем в конечном счете формулу притока (9.2.9), в которой добавочное фильтрационное сопротивление, обусловленное перфорацией выражается формулой
В формуле (9.5.6) линейные размеры принимаются в метрах. 9.5.3. Анализ формулы (9.5.6) и выбор плотности перфорации. Основными факторами, влияющими на продуктивность скважины, является глубина проникновения пуль в породу, плотность отверстий и их расположение. В работе М. Харриса [35] показано, что с увеличением глубины резко возрастает производительность скважины. Отсюда вытекает весьма важный вывод, что увеличение глубины проникновения пуль в твердых породах и улучшение техники вскрытия пласта может дать такой эффект, что по некоторым скважинам отпадет необходимость в производстве дорогостоящего гидравлического разрыва пласта.
 = 30,5 см – интервал между двумя горизонтальными плоскостями, n =1 – число отверстий, приходящееся на один интервал (на одну плоскость) или т =3 отв./м, = 30,5 см – интервал между двумя горизонтальными плоскостями, n =1 – число отверстий, приходящееся на один интервал (на одну плоскость) или т =3 отв./м,  =1, æ;*=1. =1, æ;*=1.
Заметим, что в основу метода М. Харриса положенасхема перфорации по горизонтальным плоскостям, которые могут располагаться произвольно, на различных расстояниях друг от друга и расчет производится для каждого интервала без учета взаимодействия остальных. Формула (9.5.6) учитывает взаимодействие работающих плоскостей, анизотропию и относительное вскрытие пласта при схеме равномерной перфорации пласта. Сравнение может быть сделано только при условии Графики В.И. Щурова ограничены глубиной прострела, малой точностью графического определения коэффициента С 0 и многофакторностью, что не позволяет приводить графики в широком диапазоне переменных параметров [31]. Приведенные эмпирические формулы В.И. Щурова [39] не отражают изменения глубины прострела и радиуса скважины, а потому не могут дать правильных результатов. В процессе бурения, освоения и ремонтных работ (глушение скважин) рабочие жидкости проникают в призабойную зону и вносят глинистые и цементные частицы, засоряющие поры пласта и ухудшающие его проницаемость. Последнее приводит к снижению продуктивности скважины на 5-95% от ее потенциальной величины в зависимости от глубины перфорационного канала. С целью повышения производительности скважин при освоении или в процессе эксплуатации производят перфорацию колонны и продуктивного пласта. Установлено, что в условиях загрязненной призабойной зоны несколько глубоких перфорационных каналов будут более эффективны, чем множество мелких. Особенно это характерно при вскрытии плотных трещинных коллекторов с низкой проницаемостью и пластов незначительной толщины. В промысловой практике существует несколько способов перфорации продуктивных пластов в обсаженных скважинах: кумулятивный, пулевой, торпедный, структурный и механический. Кумулятивная и торпедная перфорации являются наиболее эффективными и распространенными в условиях средних глубин скважин. Однако практика показывает, что наряду с положительными качествами (простота и дешевизна работ) эти способы не гарантируют качественных показателей вскрытия пласта (до 30—40% пуль не пробивают колонну, нарушают ею и цементный камень). Для глубокозалегающих пластов эти способы недостаточно эффективны, так как с увеличением температуры пробивная способность зарядов снижается. Как высокоэффективный метод вскрытия пласта на промыслах страны получил способ гидропескоструйной перфорации [44-46]. Техника современного вскрытия пласта позволяет создавать каналы длиной от 155-250 мм (ПКС-105 и др.) до 100 см. Плотность перфорации составляет 10-25 отв./пог. м. Слишком высокая плотность может привести к деформации и смятию обсадной колонны и разрушению цементного кольца, что приведет в свою очередь к прорыву подошвенной воды или газа к забою скважины. Малая плотность не обеспечит достаточного притока из-за высоких местных сопротивлений вблизи отверстия. Опыты показали [44, 45], что гидропескоструйная перфорация с давлением порядка 200 МПа оказывается наиболее эффективной по сравнению с другими методами. Она позволяет создавать каналы глубиной более одного метра, способствует более качественному вскрытию пласта при заканчивании скважин и интенсификации притока. В связи с этим возникает необходимость определения эффективности вскрытия продуктивных пластов в зависимости от плотности перфорационных отверстий и глубины создаваемых каналов. В литературе широко представлен анализ зависимости коэффициента совершенства h от плотности перфорации [1, 10, 39, 44, 45 и др.). Поскольку формула для коэффициента
При исходных данных в приведенном примере для l 0=34,56 см получаем из формулы (9.5.7 ) т опт = 13 отв./пог. м, при l 0=29,8 см имеем т опт=26, при l 0=100 см – т опт=2. Как видим, оптимальные условия перфорации, характеризующие обсаженную скважину как эквивалентную совершенной, обусловливаются не только числом прострелов, но и глубиной создаваемых каналов. Анализ формулы (9.5.7) показывает, что при l 0<4 r c обеспечить практически дебит эквивалентной совершенной скважины путем увеличения числа прострелов m невозможно, так как это теоретически ведет к т
Рис. 9.15. Зависимость оптимальной плотности перфорации топт от анизотропии пласта æ;* при фиксированной глубине l 0 пулевого канала (см)
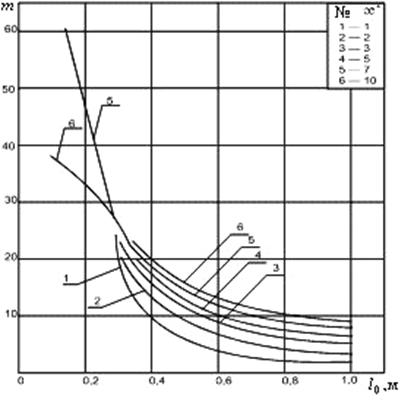
Рис. 9.16. Зависимость плотности перфорации m от глубины пефорационного канала при фиксированном значении анизотропии пласта æ;* На рис. 9.17 представлены зависимости С 0= f (l 0, m, æ;*), рассчитанные по формуле (9.5.6), из которых видно, что при увеличении глубины пулевого канала l 0 и уменьшении анизотропии пласта æ;* добавочные фильтрацион ные сопротивления C 0 уменьшаются и при определенных условиях могут оказаться отрицательными, вследствие чего дебит скважины пвышается. При большом количестве отверстий теоретически (т
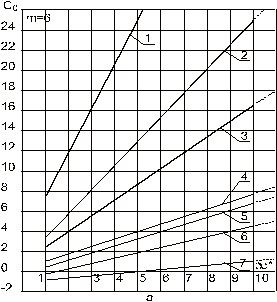
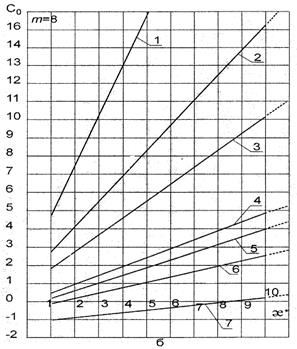
Рис.9.17.(а, б, в, г). Зависимость добавочных фильтрационных сопротивлений С 0= f (m, l 0, æ;), обусловленных перфорацией колонны при фиксированных значениях глубины канала l 0: 1 — l 0 = 0,05; 2 — l 0 = 0,10; 3 — l 0 = 0,15; 4 — l 0 = 0,30; 5 — l 0 = 0,35; 6 — l 0 = 0,50; 7 — l 0 = 1,0 м и плотности перфорации т отв. /пог. м: а — 6; б — 8; в — 10;.
|

 ; (9.5.1)
; (9.5.1) , (9.5.2)
, (9.5.2) с – угол, под которым видно прямоугольное отверстие высотой
с – угол, под которым видно прямоугольное отверстие высотой 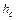 с оси скважины в горизонтальном сечении;
с оси скважины в горизонтальном сечении;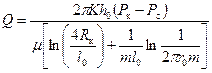 , (9.5.3)
, (9.5.3)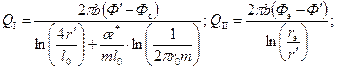 (9.5.4)
(9.5.4) ; (9.5.5)
; (9.5.5)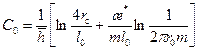 . (9.5.6)
. (9.5.6)
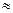 2,5, по формуле (9.5.6) при т =3 получаем С 0=1,90. Для глубины канала l 0=34,5 см. графики В.И. Щурова в литературе не приводятся. Для глубины канала l 0=3,75 см при тех же исходных данных по графикам В.И. Щурова [39] находим С 0
2,5, по формуле (9.5.6) при т =3 получаем С 0=1,90. Для глубины канала l 0=34,5 см. графики В.И. Щурова в литературе не приводятся. Для глубины канала l 0=3,75 см при тех же исходных данных по графикам В.И. Щурова [39] находим С 0 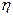 включает в себя член
включает в себя член  , который, вообще говоря, трудно определяется практически, то значение его будет неоднозначно, а потому использование его целью определения оптимального числа перфорационных каналов не даст правильных результатов. Выбор оптимального числа каналов и глубины прострела может быть сделан эффективнее, если исходить из наименьшего добавочного фильтрационного сопротивления С 0. Принимая в формуле (9.5.6) С 0=0, что соответствует притоку к эквивалентной совершенной скважине с определенными параметрами r 0и l 0, получаем
, который, вообще говоря, трудно определяется практически, то значение его будет неоднозначно, а потому использование его целью определения оптимального числа перфорационных каналов не даст правильных результатов. Выбор оптимального числа каналов и глубины прострела может быть сделан эффективнее, если исходить из наименьшего добавочного фильтрационного сопротивления С 0. Принимая в формуле (9.5.6) С 0=0, что соответствует притоку к эквивалентной совершенной скважине с определенными параметрами r 0и l 0, получаем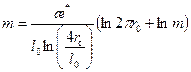 . (9.5.7)
. (9.5.7)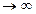 . В этом случае, очевидно, оптимальное число прострелов будет определяться прочностью колонны и характером изменения добавочного сопротивления (9.5.6). Начало выхода на монотонность изменения зависимости
. В этом случае, очевидно, оптимальное число прострелов будет определяться прочностью колонны и характером изменения добавочного сопротивления (9.5.6). Начало выхода на монотонность изменения зависимости  определит оптимальные параметры перфорации. По трансцендентному уравнению (9.5.7) при фиксированных значениях 2 r 0=0,127 м и 2 r с=0,15 м построены графические зависимости функции т = f (æ;*, l 0) (рис. 9.15 и рис. 9.16). Из анализа графиков видно, что при увеличении анизотропии пласта æ;* оптимальная плотность перфорации т опт (число отверстий на 1 пог. м) увеличивается; анизотропия пласта требует более плотной перфорации колонны. При длине нулевых каналов l 0
определит оптимальные параметры перфорации. По трансцендентному уравнению (9.5.7) при фиксированных значениях 2 r 0=0,127 м и 2 r с=0,15 м построены графические зависимости функции т = f (æ;*, l 0) (рис. 9.15 и рис. 9.16). Из анализа графиков видно, что при увеличении анизотропии пласта æ;* оптимальная плотность перфорации т опт (число отверстий на 1 пог. м) увеличивается; анизотропия пласта требует более плотной перфорации колонны. При длине нулевых каналов l 0 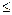 0,15 м и 1
0,15 м и 1