Основы дифференциального и интегрального методов обработки кривых восстановления давления в пласте
Гидродинамические методы исследования скважин основываются на решении известного уравнения пьезопроводности [19, 22] при фильтрации жидкости в пористой среде. Для притока однородной жидкости по линейному закону фильтрации к кольцевому стоку радиуса а в полубесконечном однородном по проницаемости пласте с непроницаемой кровлей, вскрытом на глубину h, при постоянном давлении Р 0= const на бесконечности и переменном дебите Q (t) М. Маскет дал впервые [1] точное решение для распределения давления в пласте, вызванного работой кольцевого стока. И.А. Чарный другим путем получил аналогичное решение для притока к кольцевой галерее при переменном дебите, которое записывается в виде [22]: Полагая а =0 и принимая реальную скважину за линию стоков радиуса r = r c, применив теорему о свертках, И.А. Чарный получает из уравнения (10.2.1) приближенную формулу для восстановления давления после закрытия скважины: где Р с(0) – давление на забое после остановки скважины, t =0; Р с(t) – нарастающее давление на забое после остановки скважины. Непосредственно формула (10.2.2) не может быть использована для интерпретации КВД, т. к. она не дает прямолинейной анаморфозы. Делая некоторые преобразования и упрощения, авторы [22, 56] окончательно получают: где Q – дебит в момент закрытия скважины, t =0; q (t) – затухающий дебит скважины после ее закрытия. При мгновенном прекращении притока (закрытие скважины на забое) Q (t)= Q (t)= const имеем j (t)=ln t и формула (10.2.3) переходит в известную формулу для притока жидкости к скважине (линии стоков) при Q (t)= Q = const Формулы (10.2.3) и (10.2.5) представляют собой уравнения прямых в координатах которые позволяют определять коэффициенты гидропроводности и пьезопроводности пласта. Этот метод обработки КВД называют дифференциальным. В основе интегрального метода лежит понятие импульса депрессии, введенного И.А. Чарным [22], Обозначая через V (t) суммарный накопленный объем жидкости, поступивший из пласта в скважину за время исследования после ее закрытия, и подставляя (10.2.2) в формулу (10.2.7), после некоторых преобразований И.А. Чарный дает уравнение притока в виде: где Qt – объем жидкости, который бы поступил за время t после закрытия скважины на устье, если бы скважина работала с постоянным дебитом Q; V 0(t) – фактический объем жидкости, поступивший в скважину за время t при затухающем дебите q (t). Изложенный интегральный метод также позволяет определять параметры пласта путем построения преобразованной КВД по формуле (10.2.9) в координатах Приведенные методы и их модификации широко известны в теории и практике гидрогазодинамических исследований скважин и подробно изложены в литературе. В связи с тем, что эти методы требуют достаточно трудоемких вычислений интегралов (10.2.4) и (10.2.10) и выполнения большого объема предварительных промысловых исследований, различными авторами делались удачные и неудачные попытки упростить методы, т. е. избежать интегрирования функций (10.2.4) и (10.2.10). Подчас такие упрощения оказывались грубыми и примитивными, не представляющими практического интереса, и естественно не получившими признания.
|

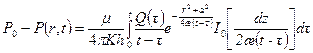 . (10.2.1)
. (10.2.1)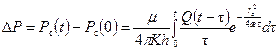 , (10.2.2)
, (10.2.2) , (10.2.3)
, (10.2.3)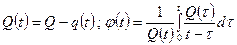 , (10.2.4)
, (10.2.4)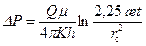 . (10.2.5)
. (10.2.5) соответственно с угловым коэффициентом b и отрезком α;, отсекаемым на оси ординат:
соответственно с угловым коэффициентом b и отрезком α;, отсекаемым на оси ординат: , (10.2.6)
, (10.2.6)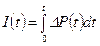 . (10.2.7)
. (10.2.7) , (10.2.8)
, (10.2.8)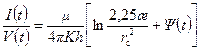 , (10.2.9)
, (10.2.9) ; (10.2.10)
; (10.2.10)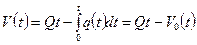 ; (10.2.11)
; (10.2.11) .
.


