Определение радиуса кольцевой неоднородности по КВД при дренировании однородно-анизотропного пласта несовершенной скважиной
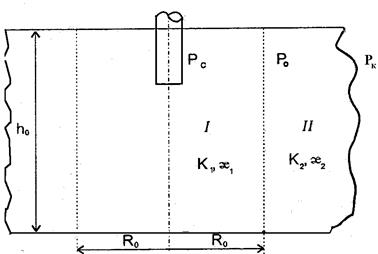
10.5.1. Пласт неограниченный. Рассмотрим приток жидкости к несовершенной скважине в неограниченном по протяженности пласте с кольцевой неоднородностью. Введем параметры K 1, æ;1 и K 2, æ;2 — горизонтальные проницаемости и пьезопроводности прискважинной и удаленной зон (рис. 10.2).
Рис.10.2. Двухзонная схема притока к скважине Для неустановившегося движения в зоне II имеем Для квазиустановившегося движения в зоне I и неустановившегося движения в зоне II справедливо соотношение или где R 0 – радиус зоны I ухудшенной проницаемости; r с пр – приведенный радиус скважины. Сделав некоторые преобразования, из (10.5.2) получаем: Решая совместно уравнение прямых (10.5.1) и (10.5.3) для точки пересечения, соответствующей t = t 0, после ряда преобразований получаем формулу: Замечая по КВД (рис. 10.3), что находим Внося (10.5.5) в (10.5.4), имеем Производя аналогичные преобразования в знаменателе формулы (10.5.2) по отношению к проницаемости К 1, получаем: Решая совместно (10.5.7) и (10.5.1) при t=t о, получаем Коэффициенты гидропроводности определяются по ломаной кривой c двумя углами наклона: Рис.10.3. Схема поведения КВД в пласте с зональной
|

 . (10.5.1)
. (10.5.1)
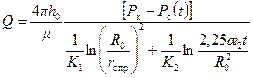 , (10.5.2)
, (10.5.2)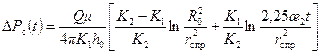 . (10.5.3)
. (10.5.3) . (10.5.4)
. (10.5.4)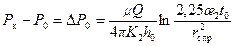 ,
,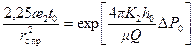 . (10.5.5)
. (10.5.5)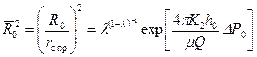 . (10.5.6)
. (10.5.6) . (10.5.7)
. (10.5.7) . (10.5.8)
. (10.5.8) . (10.5.9)
. (10.5.9)



