Неоднородностью
Коэффициенты пьезопроводности находятся по отрезку, отсекаемому экстраполированными прямыми на оси: Приведенный радиус определяется по формуле: где С 0 – добавочное фильтрационное сопротивление, обусловленное перфорацией колонны; Так как при t = t 0 имеем r = R c и æ;1= æ;2, то из (10.5.10) с учетом (10.5.9) следует Тогда формулы (10.5.6) и (10.5.7) принимают вид:
10.5.2. Пласт ограниченный. Для прискважинной зоны справедливо уравнение притока: где по И.А. Чарному [22] по Г.И. Баренблатту [43] Внешнюю зону (см. рис. 10.2) будем считать неограниченной, тогда с учетом (10.5.16) можно записать соотношение: откуда следует Производя ряд преобразований и решая (10.5.19) относительно R 0, получаем или Другой вид формул: или где Из уравнений (10.5.21) и (10.5.23) имеем Уравнения (10.5.20)-(10.5.23) относительно Из (10.5.16) находим Внося (10.5.23) в (10.5.26) с учетом (10.5.27), получаем окончательно выражение для кольцевой зоны.
Производя аналогичные операции с уравнением (10.5.23), получаем
|
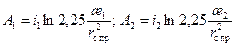. (10.5.10)
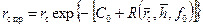, (10.5.11)
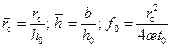; (10.5.12)
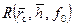– функция сопротивления при неустановившемся притоке.
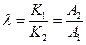. (10.5.13)
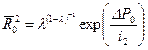. (10.5.14)
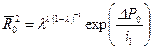. (10.5.15)
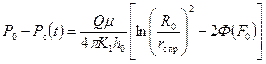, (10.5.16)
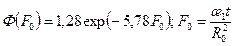; (10.5.17)
. (10.5.18)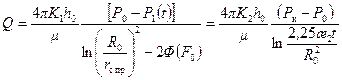
,
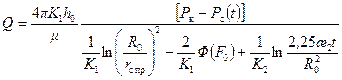. (10.5.19)
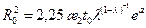(10.5.20)
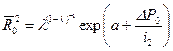. (10.5.21)
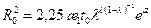(10.5.22)
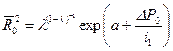, (10.5.23)
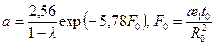. (10.5.24)
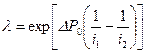. (10.5.25)
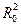являются трансцендентными. Поэтому для нахождения 
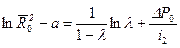. (10.5.26)
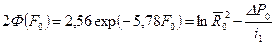. (10.5.27)
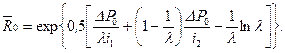(10.5.28)
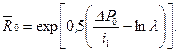(10.5.29)
